Теорема Гюйгенса – Штейнера

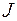Момент инерции тела относительно произвольной оси равен сумме момента инерции 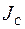относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния a между осями.

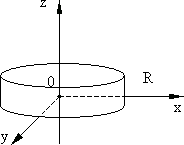
Рис. 5.11.

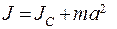(5.23)

Гюйгенс Христиан (1629 – 1695), голландский физик, механик, математик и астроном, родился в Гааге, учился в университетах Лейдена. Физические исследования в области механики, оптики, молекулярной физики. Решил задачу об определении центра колебаний физического маятника и его периода колебаний, установил законы, определяющие центростремительную силу. Исследовал столкновение упругих тел и вывел его законы.

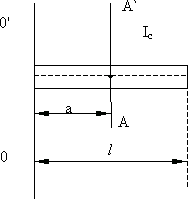
Пример: Найти момент инерции стержня относительно оси OO’, проходящей через край стержня перпендикулярно его оси (рис. 5.12):

.

.

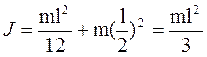Рис. 5.12.

Момент силы

Моментом силы, действующей на материальную точку, относительно начала координат (рис. 5.13), называется вектор

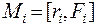(5.24)

Продифференцируем момент импульса материальной точки (5.15) по времени

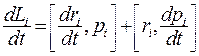(5.25)

Вектор 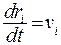является скоростью, которая совпадает по направлению с импульсом p_i, поэтому векторное произведение их равно нулю. Соотношение (5.25) запишем в виде

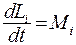(5.26)

где 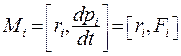- момент силы.

Уравнение (5.26) называется уравнением моментов для материальной точки.

Моментом силы твердого тела относительно начала отсчета 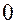называется сумма моментов сил, приложенных к точкам системы относительно начала отсчета:

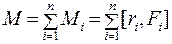(5.27)

Сила F_i,действующая на i- ую точку системы, слагается из внешней силы F_iвнеш и суммы внутренних сил f_ij:

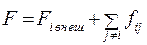(5.28)

Запишем момент сил в виде

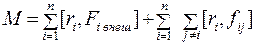(5.29)

Моменты всех внутренних сил равны нулю, т.к. силы взаимодействия любых двух материальных точек равны по величине и противоположны по направлению. Таким образом, момент всех сил равен суммарному моменту внешних сил:

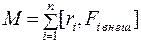(5.30)

Продифференцируем момент импульса системы материальных точек L (5.16) по времени и получим уравнение моментов для твердого тела

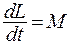(5.31)

где M - момент внешних сил.

Пусть ось вращения тела z является одной из главных осей инерции. Найдем проекцию момента импульса системы на ось z

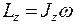(5.32)

Продифференцируем (5.32) по времени

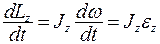(5.33)

Проекцию момента всех сил на ось z обозначим M_z. Уравнение моментов относительно оси z запишем в виде

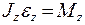(5.34)