Гармонические колебания

Наиболее простыми являются собственные колебания системы, происходящие по закону синуса или косинуса. Эти колебания называются гармоническими. Они возникают под действием внутренней силы, называемой квазиупругой силой (т.е. как бы упругой):

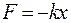(7.1)

Частота и амплитуда гармоничеcких колебаний остаются постоянными.

Возьмем шарик массой m, закрепленный на конце пружины длиной 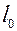. Под действием силы тяжести пружина растянется, ее длина станет равной 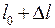(рис. 7.1). При этом возникнет сила упругости, направленная в сторону, противоположную направлению растяжения:

,

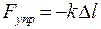где 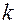- жесткость пружины.

Потянем за шарик и отпустим. Длина пружины станет равной 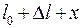, где x - отклонение от положения равновесия. На шарик будет действовать сила тяжести 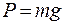и сила упругости

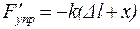
Результирующая сила равна сумме этих сил:

.

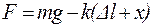Сила тяжести P и сила упругости 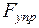в положении равновесия равны между собой:

.

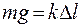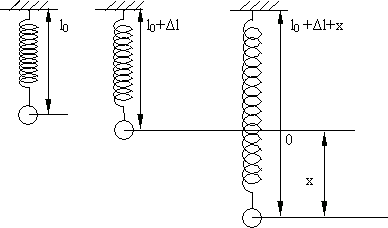
Рис. 7.1.

Согласно второму закону Ньютона, силу можно записать в виде 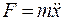, где точками обозначена вторая производная по времени, что позволяет записать дифференциальное уравнение

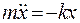(7.2)

Разделим левую и правую части уравнения на массу m и запишем уравнение гармонических колебаний

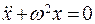(7.3)

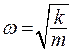(7.4)

Это уравнение является однородным линейным дифференциальным уравнением второго порядка. Его решение

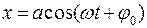(7.5)

где a - наибольшее отклонение колеблющейся величины x от положения равновесия, называемое амплитудой колебаний;

w - циклическая частота колебаний; 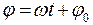- фаза колебаний;

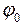- начальная фаза.

Поскольку 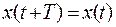, то 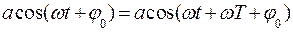. Отсюда получаем, что 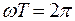, следовательно, период колебаний:

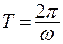(7.6)

График представлен на рис. 7.2.

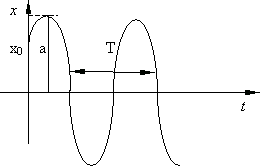
Рис. 7.2.

Число колебаний за единицу времени 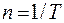. В системе СИ [n] = 1/с = Гц. Между циклической частотой w и частотой n существует связь:

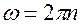(7.7)

По известным значениям начальной фазы j₀ и амплитуды колебаний можно найти начальное отклонение от положения равновесия 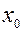и начальную скорость :

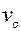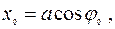
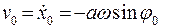(7.8)

Возможно и обратное решение:

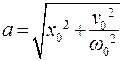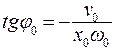, . (7.9)

Квазиупругая сила является консервативной силой, поэтому в замкнутой системе должна сохраняться полная механическая энергия:

,

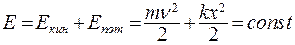где полную механическую энергию можно записать в виде

.

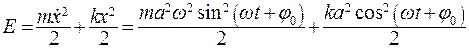Поскольку 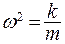, получим полную энергию:

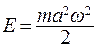(7.10)

При движении потенциальная энергия переходит в кинетическую, и наоборот. Кинетическая и потенциальная энергии имеют вид

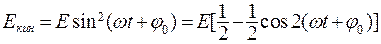
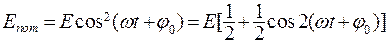(7.11)

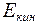и 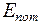изменяются с частотой 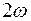, в два раза большей, чем частота колебаний w, среднее значение кинетической энергии 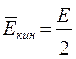, и потенциальной 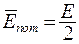, таким образом, средние значения их равны между собой:

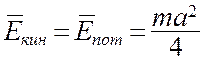(7.12)