Кинетическая энергия вращающегося твердого тела

Пусть твердое тело имеет переносную скорость u = 0, т.е. не совершает поступательного движения, тогда из (5.2) следует, что скорость его точек равна

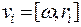(5.35)

где w- мгновенная угловая скорость вращения.

Кинетическая энергия вращающегося твердого тела равна

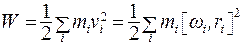(5.36)

Если оси системы координат направить вдоль главных осей инерции тела, то энергию можно записать в виде

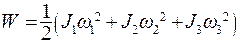(5.37)

Если ось вращения совпадает с одной из главных осей:

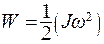(5.38)

Пусть теперь переносная скорость тела 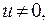тогда кинетическая энергия равна

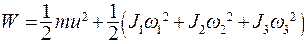(5.39)

Например, кинетическая энергия цилиндра радиусом R, катящегося со скоростью u

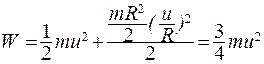(5.40)

ГЛАВА 6. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Закон сохранения момента импульса

Моментом импульсаL_iматериальной точки с массой 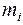, движущейся со скоростью n_i относительно начала координат 0, называется векторное произведение радиус-вектора r_i на вектор импульса p_i:

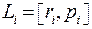(6.1)

Вектор L_i перпендикулярен к векторам r_i иp_i (рис. 6.1).

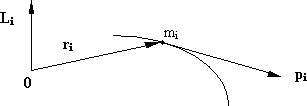
Рис. 6.1.

Моментом импульса механической системы относительно начала координат 0 называется вектор L, равный геометрической сумме моментов импульсов всех материальных точек относительно точки О.

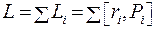(6.2)

Значение момента импульса зависит от выбора начала координат. Если начала координат отстоят на расстоянии a друг от друга (рис. 6.2), то радиус-векторы одной и той же точки связаны соотношением

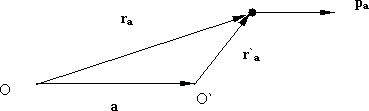
Рис. 6.2.

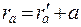(6.3)

Поэтому момент импульса системы

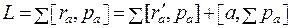(6.4)

или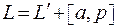

Отсюда следует, что момент импульса не зависит от выбора начала координат только в том случае, когда система покоится как целое, и ее суммарный импульс равен нулю: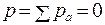

Продифференцируем по времени выражение (6.2), получим

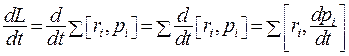(6.5)

так как

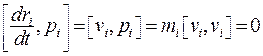
Согласно второму закону Ньютона

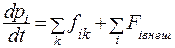(6.6)

где f_ik - внутренние силы, действующие на материальную точку с массой ;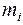

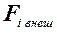- внешние силы. Из (6.5) получим

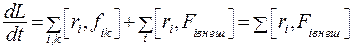(6.7)

так как суммарный момент внутренних сил равен нулю, .

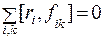Вектор 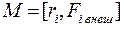называется главным моментом всех внешних сил, действующих на механическую систему.

Таким образом, из уравнения моментов

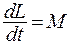(6.8)

следует, что поскольку для замкнутой системы момент импульса внешних сил 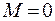, то 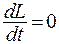и выполняется закон сохранения момента импульса:

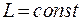(6.9)

Момент импульса замкнутой системы относительно неподвижнойточки не изменяется с течением времени.

Законы сохранения энергии, импульса и момента импульса выполняются не только для механических систем, но и для систем атомов и молекул, атомных ядер и элементарных частиц. В отличие от макроскопического тела, момент импульса которого связан с движением относительно некоторой точки или оси, микрочастица может обладать также собственным моментом импульса, называемым спином. Полный момент импульса микрочастицы L_i равен сумме орбитального момента импульса L_ir и собственного момента импульса L_is:

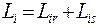(6.10)