Движение твердого тела

Твердым телом называется система материальных точек, расстояние между которыми остается постоянным. Твердое тело можно определить как тело, деформациями которого можно пренебречь. Основными видами движения в природе являются: поступательное и вращательное. Всякое движение можно разложить на эти виды движения. Примером может служить цилиндр, скатывающийся с горки (рис. 5.1).

Рис. 5.1.

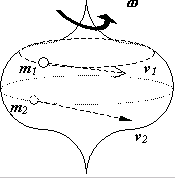
Поступательное движение твердого тела характеризуется тем, что все точки тела движутся со скоростью, одинаковой по величине и направлению (рис. 5.2).

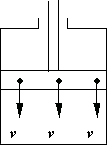
Вращательноедвижение отличается тем, что все точки тела движутся с одинаковой угловой скоростью по концентрическим окружностям, центры которых расположены на оси вращения. Линейные скорости материальных точек различны (рис. 5.3).

Рис. 5.2.	Рис. 5.3.

Колебательное движение характеризуется периодичностью, его можно рассматривать как часть вращательного движения.

Рассмотрим сложное движение материальной точки относительно неподвижной системы отсчета (рис. 5.4). Его можно представить как вращение с угловой скоростью w в системе отсчета, движущейся относительно неподвижной системы поступательно со скоростью u

Поскольку линейная скорость n¢ точки с радиус - вектором r вращающейся с угловой скоростью wзаписывается в виде

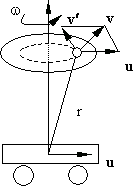
Рис. 5.4.

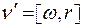(5.1)

то скорость точки при сложном движении

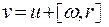(5.2)

Для описания движения каждой точки твердого тела необходимо применить второй закон Ньютона:

(5.3)

где f - результирующая всех внутренних сил, действующих на данную точку с массой ;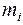

F_iвнеш - результирующая внешних сил.

Запишем сумму этих уравнений

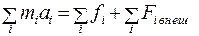(5.4)

Cумма внутренних сил в твердом теле равна нулю, т.к., согласно третьему закону Ньютона, любые две точки твердого тела действуют друг на друга с силами, равными по величине и противоположными по направлению (рис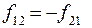. 5.5):

(5.5)

Поэтому уравнение (5.4) запишем в виде

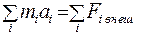(5.6)

Степени свободы

Числом степеней свободы системы материальных точек называется число независимых параметров, позволяющих полностью задать положение системы в пространстве.

Если твердое тело состоит из n материальных точек, то необходимо задать 3 n координат, но эти координаты не являются независимыми. Возьмем одну материальную точку в декартовой системе координат. Очевидно, что число степеней свободы будет равно 3, т.к. необходимо задать 3 координаты точки. Если две материальные точки жестко связаны между собой, то число степеней свободы i = 2×3-1 = 5

Число степеней свободы твердого тела i = 6 т.к. для жесткого закрепления тела необходимо задать координаты трех точек и вычесть три жестких связи между ними.

Можно разделить число степеней свободы твердого тела на сумму трех степеней свободы, связанных с описанием поступательного движения и трех степеней свободы, соответствующих вращательному движению вокруг трех осей. Углы поворота вокруг этих осей называются углами Эйлера.

Эйлер Леонард (1707 – 1783), математик, механик и физик, родился в г. Базеле (Швейцария), учился в Базельском университете. В 1727 г. по рекомендации братьев Николая и Даниила Бернулли начал работать в Петербургской АН. Исследования относятся ко многим разделам математики: теории функций комплексного переменного, вариационного исчисления, теории специальных функций. Работы Эйлера в физике посвящены механике, оптике, акустике, теплоэлектричеству. Ввел понятие «эфира», в оптике создал собственную волновую теорию света. Установил закон сохранения импульса (1746), развил теорию моментов инерции. Наряду с Д.Бернулли является создателем механики жидкостей и газов.

Центр масс

Центром масс, или центром инерции системы материальных точек, называется точка, положение которой задается радиус-вектором:

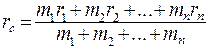(5.7)

Для случая двух материальных точек, расположенных на оси x (рис. 5.6):

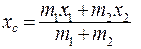(5.8)

где 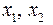- координаты точек с массами 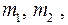соответственно;

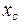- координата центра масс.

Покажем, что центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к телу сил. Найдем сначала скорость центра масс, для этого продифференцируем (5.7) по времени

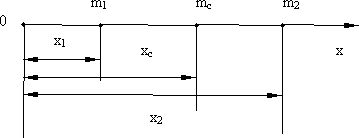
Рис. 5.6.

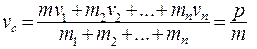(5.9)

где p - суммарный импульс всех материальных точек тела.

Ускорение центра масс

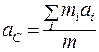(5.10)

Если записать второй закон Ньютона для всех точек твердого тела в виде (5.6), то находим

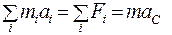(5.11)

отсюда следует

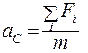(5.12)

Ускорение, с которым движется центр масс твердого тела, равно отношению результирующей внешней силы к массе тела.

Движение твердого тела можно рассматривать как движение его центра масс. Поскольку в замкнутой системе сумма внешних сил равна нулю, 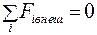, то 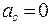Внутренние силы не могут изменить скорость движения центра масс, поэтому в замкнутой системе

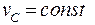(5.13)

Момент импульса

Закрепим твердое тело в точке О (рис. 5.7). Угловая скорость вращения твердого тела w Радиус-вектор точки m_i относительно О обозначим r_i Скорость i- ой точки тела

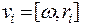(5.14)

Моментом импульса материальной точки относительно точки О называется векторное произведение радиус-вектора r_i на вектор импульса p_i:

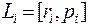(5.15)

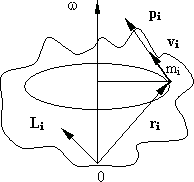
Рис. 5.7.

Момент импульса L всего тела относительно точки О равен

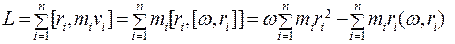(5.16)

Моментом импульса относительно оси называется проекция вектора L а эту ось. Запишем (5.16) в виде трех проекций на оси декартовой системы координат:

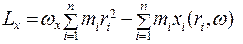
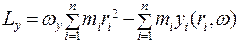(5.17)

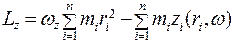
С учетом того, что 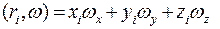из (5.17) получим

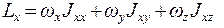
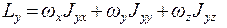(5.18)

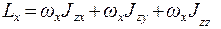
где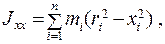

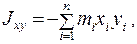
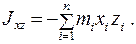
Аналогично находим остальные величины.

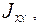
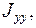
Величины 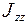называются осевыми моментами инерции, а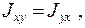 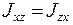и 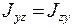- центробежными моментами инерции.

Момент импульса материальной точки перпендикулярен радиус-вектору r_i и вектору импульса 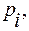направление его не совпадает с направлением угловой скорости w (рис. 5.8).

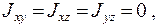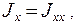
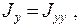
Момент импульса твердого тела сложным образом зависит от распределения масс в теле. Если то величины 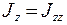называются главными моментами инерции относительно главных осей, совпадающих с осями координат.

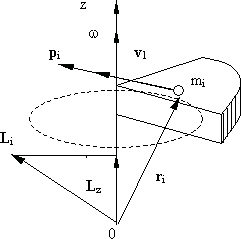
Рис. 5.8.