Применение закона сохранения момента импульса

ОПЫТ 1.Скамья Жуковского представляет собой диск, вращающийся без трения вокруг оси, перпендикулярной к плоскости диска. Пусть в начальный момент в центре скамьи Жуковского радиусом R и массой 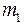находился шар радиусом r и массой 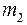(рис. 6.3). Затем в процессе вращения под действием внутренних сил он перекатился на край скамьи (рис. 6.4).

С какой угловой скоростью 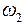будет теперь вращаться система, если начальная угловая скорость ее ?

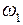Найдем момент инерции системы 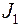относительно оси OO' в начальный момент времени

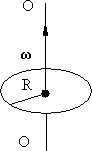
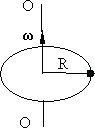
Рис. 6.3. Рис. 6.4.

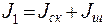
где 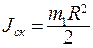- момент инерции скамьи Жуковского,

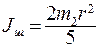- момент инерции шара.

Момент инерции системы после того, как шар перекатился на край диска, запишем в виде

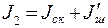
где 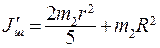- момент инерции шара на краю скамьи. Запишем закон сохранения момента импульса системы

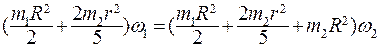(6.15)

Найдем угловую скорость вращения системы в конечный момент времени:

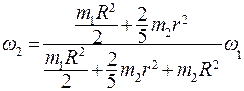(6.16)

Угловая скорость 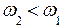, т.к. увеличился момент инерции системы ( 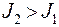). Закон сохранения механической энергии в этом случае не выполняется, т.к. изменяется внутренняя энергия системы за счет изменения кинетической энергии:

.

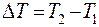Кинетическая энергия вращающегося тела

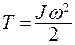(6.17)

Изменение кинетической энергии системы

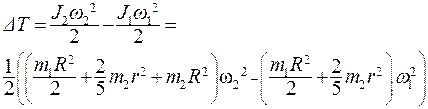(6.18)

ОПЫТ 2. Платформа, на краю которой стоит человек, вращается с угловой скоростью 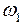. Человек начинает идти по краю платформы со скоростью n в направлении, противоположном движению платформы. Какова будет угловая скорость платформы 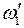относительно неподвижной системы отсчета? Масса платформы 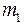, масса человека 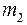, радиус платформы R.

Система, состоящая из платформы и человека, является замкнутой, следовательно, выполняется закон сохранения момента импульса относительно неподвижной системы отсчета:

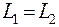(6.19)

Если считать, что масса человека сосредоточена в одной точке, то момент инерции системы в начальный момент

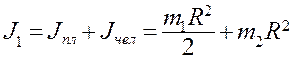(6.20)

Начальный момент импульса относительно оси вращения z

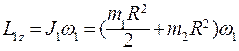(6.21)

После того, как человек пойдет по платформе, момент импульса системы относительно оси вращения будет равен геометрической сумме момента импульса платформы и человека относительно неподвижной системы отсчета

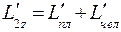(6.22)

где ,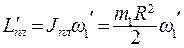

.

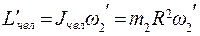Получим

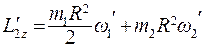(6.23)

Из закона сохранения момента импульса cледует

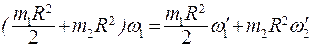(6.24)

Поскольку угловая скорость человека относительно платформы 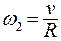, то относительно неподвижной системы

.

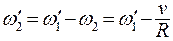Таким образом, угловая скорость платформы относительно

неподвижной системы

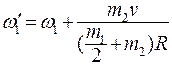(6.25)

Контрольные вопросы:

1. Сложное движение твердого тела. Характеристики поступательного, вращательного и колебательного движений.

2. Число степеней свободы твердого тела.

3. Момент силы материальной точки. Момент силы твердого тела относительно точки и оси. Момент инерции материальной точки. Момент импульса материальной точки. Условия сохранения момента импульса системы.

4. Механическая энергия. Кинетическая энергия. Потенциальная энергия. Закон сохранения механической энергии замкнутой системы тел.

5. Импульс. Закон сохранения импульса замкнутой системы тел. Закон сохранения момента импульса для вращательного движения замкнутой системы тел.