СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
Как мы уже говорили, закон распределения или плотность распределения несёт полную информацию о случайной величине.
На практике довольно часто требуется сравнить две случайные величины. Довольно полно это можно сделать, если сопоставить графики их законов или плотностей распределения.
Но в большинстве случаев желательно, чтобы итог сравнения выражался количественно, т.е. числом, а не просто общим впечатлением от вида графиков.
Поэтому хотелось бы иметь числовые характеристики, которые бы описывали существенные черты закона распределения или плотности распределения, причём любого вида.
Наиболее простыми и одновременно самыми важными, а поэтому самыми часто употребительными числовыми характеристиками случайных величин являются математическое ожидание (среднее) и дисперсия (рассеяние).
Кроме них существуют и другие, но они применяются реже, и мы их рассматривать не будем.
Математическое ожидание случайной величины Х является вероятностным обобщением хорошо известного всем со школы понятия среднего арифметического, которое, кстати, применяется в статистике.
Со среднего арифметического и начнём. Выразим его с помощью более общей формулы, которая позволит вычислять математическое ожидание.
Вначале рассмотрим дискретную случайную величину Х с N возможными значениями. (У кубика – 6 возможных значений.)
Пусть с этой случайной величиной проделано n одинаковых опытов («эн» маленькое). Например, кубик бросался 100 раз.
При этом случайная величина Х (икс большое)
значение 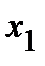 приняла
приняла 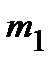 раз, т.е.
раз, т.е. 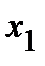 –
– 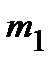 ,
,
значение 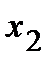 приняла
приняла 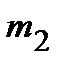 раз, т.е.
раз, т.е. 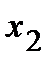 –
– 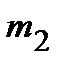 ,
,
и так далее …,
значение 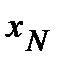 приняла
приняла 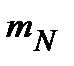 раз, т.е.
раз, т.е. 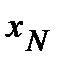 –
– 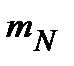 .
.
Общее количество появления всех значений равно n, т.е.
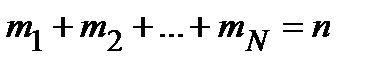
Найдём среднее арифметическое случайной величины Х по n опытам.
Среднее арифметическое – это, как известно, сумма всех значений, делённая на их количество:
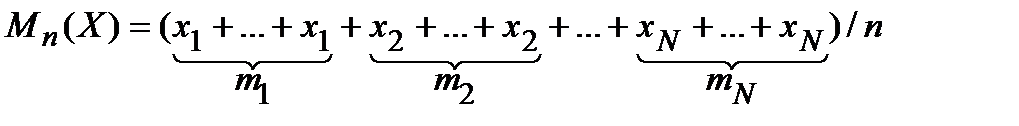 .
.
Преобразуем это выражение, учтя повторяемость значений:
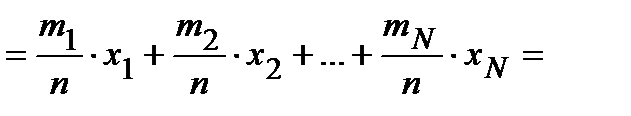
Теперь для сокращения длины формулы воспользуемся специальным знаком суммы, который мы уже рассматривали,
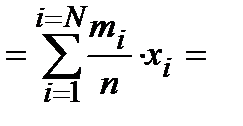
Дробь в каждом слагаемом – это вычисленная по n опытам частота события, состоящего в том, что случайная величиной Х примет значение 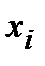 . Мы её обозначали так:
. Мы её обозначали так: 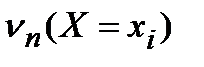 .
.
В итоге получаем:
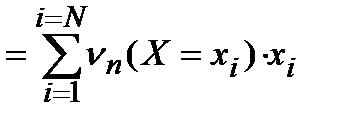
Так, введя некоторые обозначения, мы преобразовали выражение для среднего арифметического.
Из полученного выражения видно, что среднее арифметическое вычисляется как сумма значений случайной величины, взятых с множителями, в качестве которых выступают частоты 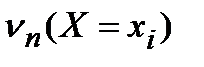 .
.
Дата добавления: 2021-01-26; просмотров: 588;











