Дисперсия случайной величины и ее свойства. Среднее квадратичное отклонение.
Кроме положения центра группирования случайной величины, о котором несет информацию математическое ожидание, важно знать разброс или рассеяние значений случайной величины относительно центра группирования.
Для этого рассмотрим разность 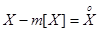 , которую называют центрированной случайной величиной или отклонением от МО, ее МО всегда равно нулю.
, которую называют центрированной случайной величиной или отклонением от МО, ее МО всегда равно нулю.
Поэтому для характеристики разброса возможных значений случайной величины пользуются не средним значением отклонения, а средним значением квадрата отклонения случайной величины от МО.
Дисперсией (рассеянием) случайной величины X называют математическое ожидание квадрата соответствующей центрированной величины:
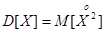 или
или 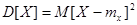 .
.
Из определения дисперсии вытекают формулы для вычисления ее:
а) для случайной дискретной величины
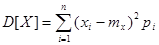 , или
, или 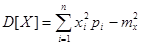 ;
;
б) для случайной непрерывной величины
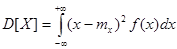 , или
, или 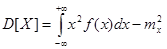 .
.
Дисперсия позволяет оценивать кучность (разброс) значений случайной величины около ее математического ожидания и является неслучайной величиной.
Свойства дисперсии:
а) дисперсия всегда положительна и имеет размерность квадрата размерности случайной величины;
б) дисперсия постоянной величины равна нулю, т.е. 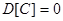 .
.
в) постоянный множитель при постоянной величине можно выносить за знак дисперсии в квадрате 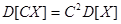 ;
;
г) величина дисперсии не зависит от начала отсчета.
Частный случай дисперсии.
Пусть случайная величина X принимает частные значения 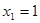 с вероятностью
с вероятностью 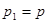 и
и 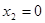 с вероятностью
с вероятностью 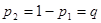 .
.
Тогда 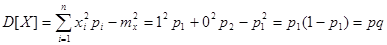 .
.
Дата добавления: 2021-11-16; просмотров: 562;











