Выборочное среднее – это оценка неизвестного значения математического ожидания наблюдаемой в опыте случайной величины.

Вычисляется по формуле среднего арифметического :

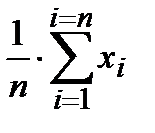= (x₁ + x₂ + … + x_n) / n = , где n – объём выборки.

– это принятое в статистике обозначение для величины, которую мы в теории вероятности обозначали как M_n(X).

Формула для выборочного среднего одинаково пригодна как для дискретных, так и для непрерывных случайных величин.

С ростом объёма выборки возможное отклонение выборочного среднего от оцениваемого неизвестного математического ожидания случайной величины M(X) уменьшается.

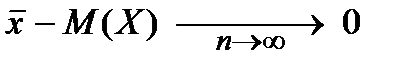
Эта и подобные ей сходимости представляют собой проявления закона больших чисел, т.е. закона больших количеств данных.

Закон больших чисел звучит так: совместное действие большого числа случайных явлений приводит к результату, почти не зависящему от случая.

Статистика

Сейчас нами изучается статистика как отрасль знаний.

Можно также услышать словосочетания: «статистика краж», «статистика убийств». Здесь под статистикой понимается совокупность данных.

Но в аналитической статистике как отрасли знаний статистика – это не только данные, а ещё это какая-либо функция от выборочных данных (в виде формулы).

Т.е. статистика – это и область знаний, и данные, и функция данных. Безусловно, неудобно, что одно и то же слово имеет разные значения, но так уж сложилось.

Статистикой, например, является выборочное среднее. А также выборочная дисперсия, выборочный коэффициент корреляции, которые будут рассмотрены позже.

Поскольку выборочные данные случайны, их различные наборы, подставленные в одно и то же выражение для статистики, каждый раз будут давать несколько отличающиеся результаты.

Поэтому статистика как функция является случайной величиной.

Её распределение, среднее и дисперсия отличаются от соответствующих характеристик выборочных данных, использованных при её вычислении.