ЗАКОН РАСПРЕДЕЛЕНИЯ

Поговорим поподробнее о дискретной случайной величине.

Дискретная случайная величина принимает в опыте одно из своих возможных отстоящих друг от друга значений.

Для того чтобы указать то, насколько часто случайная величина принимает какое-то значение, следует рассмотреть вероятность этого значения.

Рассмотрим простейший опыт с дискретной случайной величиной: бросание игрального кубика.

В этом опыте случайно количество очков, выпадающих на верхней грани кубика. Это – случайная величина, и у неё имеется 6 возможных значений: 1, 2, 3, 4, 5 и 6.

Очевидно, что если кубик правильной формы, то все грани выпадают с одинаковой вероятностью.

Чему равна вероятность каждого из возможных значений?

Игральный кубик – это идеальный пример для пояснения классического определения вероятности:

1) количество исходов конечно – 6, и исходы равновозможны,

2) вероятность каждого исхода

= 1/6 .

Сведём в таблицу все возможные значения, выпадающие при бросании кубика, и их вероятности:

Изобразим полученное соответствие между возможными значениями и их вероятностями также в виде графика. (На графике принято, что 1/6 » 0,17.)

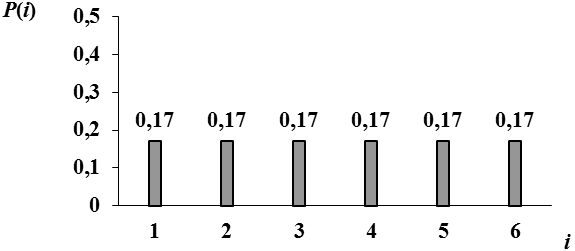
Теперь познакомимся с одним из важнейших понятий, используемых в теории вероятностей.

Законом распределения вероятности или просто законом распределения называется соответствие между возможными значениями дискретной случайной величины и их вероятностями.

Особая важность этого понятия в том, что закон распределения несёт в себе всю информацию о дискретной случайной величине.

Закон распределения может быть задан различными способами: 1) графиком, 2) таблицей, 3) формулой.

Формула для нашего простейшего случая будет следующая:

P(i) = 1/6, при i = 1, 2, …, 6 .

Основное свойство закона распределения:

сумма всех значений закона распределения равна единице.

Для нашего примера это:

P(1) + P(2) + … + P(6) = 1.

Это свойство связано с тем, что совокупность значений случайной величины соответствует полной группе событий. А вероятность суммы полной группы событий равна сумме вероятностей этих событий и равна 1.

Ещё более простой пример: бросание монеты.

Если присвоить числовые значения сторонам монеты: «орлу» - 0, а «решке» - 1, то в качестве случайной величины можно рассмотреть число, соответствующее верхней стороне упавшей монеты.

Закон распределения для монеты графически будет выглядеть так:

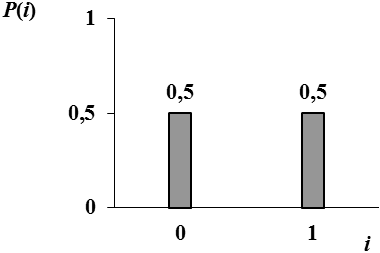
Высоты столбиков одинаковы, т.к. стороны монеты равновозможны, а значения равновероятны.

Рассмотрим теперь пример, в котором возможные значения случайной величины будут неравновероятными: сумма очков при двукратном бросании монеты.

«Орлу» ставим в соответствие 0 очков, «решке» – 1 очко.

В опыте возможно выпадение обоих «орлов», т.е.

ОО.

Тогда сумма очков будет равна 0.

Возможно выпадение первого «орла», второй «решки» или наоборот: первой «решки», а второго «орла», т.е.

ОР или РО.

В обоих случаях сумма очков будет равна 1.

И ещё возможно выпадение обеих «решек»

РР.

Сумма очков будет равна 2.

Таким образом, сумма очков при двукратном бросании монеты – это случайная величина с тремя возможными значениями: 0, 1, 2.

Вероятности этих значений легко назвать и так, но мы это сделаем с использованием классического определения вероятности.

В нашей задаче двукратного бросания имеется 4 элементарных исхода: «ОО», «ОР», «РО», «РР». Все они равновозможны.

Значение суммы в 0 очков возникает в 1-м из 4-х возможных исходов. Поэтому можем записать:

P(0) = 1/4,

где 1 – это количество элементарных исходов, соответствующих значению суммы, равному 0; 4 – это общее количество элементарных исходов.

Значение суммы очков 1 возникает при 2-х из 4-х возможных исходов, поэтому

P(1) = 2/4 = 1/2 .

Значение суммы очков 2 возникает при 1-м из 4-х возможных исходов:

P(2) = 1/4 .

Рисуем график закона распределения

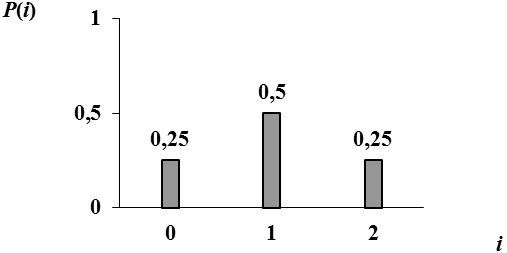
Для этого примера снова убеждаемся в справедливости основного свойства закона распределения:

P(0) + P(1) + P(2) = 1/4 + 1/2 + 1/4 = 1 .