Действующее и среднее значение периодической

Несинусоидальной величины

Как было показано выше, действующим называется среднеквадратичное за период значение величины:

.

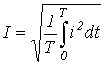При наличии аналитического выражения функции i(t) и возможности взятия интеграла от ее квадрата действующее значение i(t) определяется точно. Однако в общем случае на практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.

Пусть 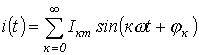. Тогда

Очевидно, что каждый из интегралов от тригонометрических функций в последнем выражении равен нулю. Таким образом,

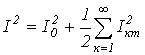
или

.

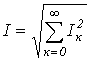Действующим значением периодической функции называется квадратный корень из суммы квадратов удерживаемых гармоник ряда Фурье.

Аналогичные выражения имеют место для ЭДС, напряжения и т.д.

Среднее значение вычисляется:

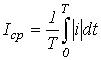
ИЛИ

Средним значением периодического несинусоидального тока называют сумму средних значений гармоник ряда Фурье данной функции.