МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

В статистике, как только что было получено, среднее арифметическое по известным результатам n опытов вычисляется так

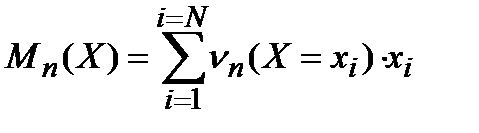
Начнём неограниченно увеличивать число опытов

n ® ¥

При этом частота каждого возможного значения случайной величины сходится к некоторому числу, называемому и являющемуся вероятностью этого значения

.

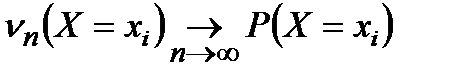А выражение для среднего арифметического переходит в выражение, которое и соответствует математическому ожиданию дискретной случайной величины

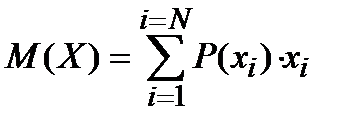
В формуле для математического ожидания вместо частот стоят вероятности значений, а возле буквы M уже не пишется буквочка n.

N (большое) – это, по-прежнему, количество возможных значений.

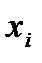– возможные значения дискретной случайной величины (их N штук).

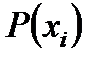– значения закона распределения дискретной случайной величины.

Математическое ожидание дискретной случайной величинывычисляется как сумма произведений всех значенийслучайной величины на их вероятности.

Смысл математического ожидания: математическое ожидание – это среднее значение случайной величины. Т.е. тот же, что и у среднего арифметического.

В теории вероятностей математическое ожидание дискретной случайной величины вычисляется без проведения каких-либо опытов по известным значениям закона распределения. Поэтому другое его название – теоретическое среднее.

Вычислим математическое ожидание для какого-нибудь простого случая: например, для опыта с монетой.

«Орлу» мы ставили в соответствие 0, а «решке» – 1.

Закон распределения для монеты, мы помним, выглядит так:

Вычисляем математическое ожидание. У нас всего два возможных значения, следовательно, меняется от 1 до 2.

i=1 соответствует «орёл», т.е. 0, а i=2 – «решка», т.е. 1. Вероятности этих обоих значений одинаковы и равны 0.5.

M(X) = 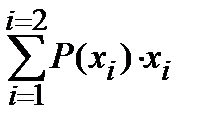= P(x₁) × x₁ + P(x₂) × x₂ = 0.5 × 0 + 0.5 × 1 = 0.5

Получилось 0.5. Что это за число?

Это число лежит посередине между возможными значениями нашей случайной величины.

Теперь более сложный предмет.

Представим, что у нас игральный кубик, у которого грани закрашены двумя красками: четыре грани – в чёрный цвет, а оставшиеся две – в белый.

В 4 случаях из 6 у кубика будет выпадать чёрная грань, а в 2 случаях — белая.

Таким образом, вероятность чёрного будет в 2/3, а белого – 1/3.

Чёрному цвету припишем значение 0; а белому – 1.

Вычислим математическое ожидание такого закона распределения.

M(X) = P(x₁) × x₁ + P(x₂) × x₂ = 2/3 × 0 + 1/3 × 1 = 1/3.

Видим, что, если получившееся значение отметить на горизонтальной оси, то оно окажется ближе к более высокому столбику. А если мы представим, что столбики сделаны из металла, то чем выше столбик, тем он тяжелее. В итоге, математическое ожидание будет расположено ближе к более тяжёлому столбику.

И сейчас пришло время познакомиться с одним важным свойством математического ожидания.

Представим такой опыт: на невесомой линейке в точках, равных значениям случайной величины, размещены гирьки с весами, пропорциональными вероятностям соответствующих значений.

Если теперь подвести под линейку опору в точке математического ожидания, то получившиеся качели или весы окажутся в равновесии.

Точка математического ожидания находится под центром тяжести таких весов.

Любопытно то, что даже если закон распределения будет сложнее, т.е. будет состоять из многих столбиков, картина будет той же.

67 г

33 г

M(X)

Таким образом, математическое ожидание дискретной случайной величины соответствует абсциссе центра тяжести закона распределения. Абсцисса – это, кто забыл, координата на горизонтальной оси.

И ещё об одном понятии, которое будет использоваться в дальнейшем.

Операция усреднения – это суммирование каких-либо значений с множителями, равными их вероятностям.

Это, как раз, та математическая операция, которая используется при вычислении математического ожидания.