РАВНОМЕРНО И НОРМАЛЬНО РАСПРЕДЕЛЁННЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

В качестве примера дискретных случайных величин нами была рассмотрены: бросание кубика и бросание монеты.

Рассмотрим теперь примеры непрерывных случайных величин.

Равномерно распределённая случайная величина.

x

p(x)

b

a

1/(b–a)

Плотность распределения такой случайной величины есть функция, отличная от нуля только в пределах отрезка от a до b.

Её уровень в пределах отрезка от a до b постоянен и обратно пропорционален длине отрезка:

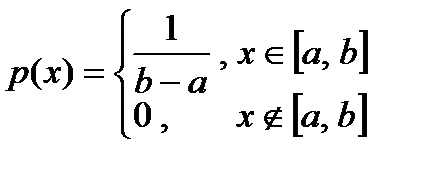
Равномерно распределённая случайная величина наиболее проста для понимания и описания.

Также как на рисунке выглядит слой, который образуют случайно вылетающие из распылителя капельки краски при нанесении изображения через трафарет.

Равномерное распределение имеют ошибки округления при измерениях или вычислениях.

Например, взвешиваем образец товара из проверочной закупки. Его масса может принимать любое значение, но мы, глядя, на шкалу весов, определяем ближайшее деление. Ошибка снятия показаний по шкале имеет равномерное распределение.

Эта случайная величина будет использоваться нами в практических работах. Датчик случайных чисел в электронных таблицах Excel выдаёт значения, равномерно распределённые в промежутке от 0 до 1.

Нормально распределённая случайная величина.

Примером нормально распределённой случайной величины является координата попадания шарика на ось в опыте с доской Гальтона, который рассматривался нами в вопросе «Первые статистические опыты».

Ещё говорят, что такая случайная величина имеет нормальное распределение.

Второе название – Гауссово распределение – по имени математика Карла Гаусса (1777-1855).

Случайные величины с нормальным распределением имеют исключительно широкое распространение в природе.

Отсюда и название: нормальное, что значит типовое, характерное.

Математическая запись нормальной плотности распределения следующая (формула страшная):

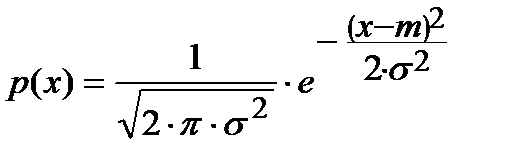, для .

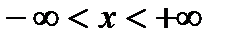Здесь p = 3,14…, а е = 2,72… – основание натурального логарифма.

Параметрами нормального распределения являются величины m и s², имеющие специальные названия:

m – математическое ожидание или среднее;

s² – дисперсия или рассеяние (обозначается маленькой греческой буквой «сигма» в квадрате).

Более подробно смысл этих понятий будет объяснён позже.

На графике плотность распределения вероятности нормально распределённой случайной величины выглядит как колоколообразная кривая.

p rqsAVSchFTzSAfrVJyFTA/IetE8p81IkPuyd3ou3552EdHLaOq/LxbOzOg1jnjVrdXay+dLMq1YV xZFhdsyIg6MRp9OSOAv+2DlqW0ACkzw4IaBw0EulzUQvDH2cFVAhYNLm6YTA6YRAd9j65Q4PcYmm 6H/l+4BYtA1qFc/Or6lVI862AjShVqFUnc62/rkO8wPm8T/k8KpQ//MQ/cdP/x7X/X9xevdfAAAA //8DAFBLAwQUAAYACAAAACEAe5lUp94AAAAJAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQWuDQBCF 74X8h2UCvTWrGyxiXUMIbU+h0KRQetvoRCXurLgbNf++k1N7Gt68x5tv8s1sOzHi4FtHGuJVBAKp dFVLtYav49tTCsIHQ5XpHKGGG3rYFIuH3GSVm+gTx0OoBZeQz4yGJoQ+k9KXDVrjV65HYu/sBmsC y6GW1WAmLredVFH0LK1piS80psddg+XlcLUa3iczbdfx67i/nHe3n2Py8b2PUevH5bx9ARFwDn9h uOMzOhTMdHJXqrzoWKdrTvJUCgT7SXJfnDQolSqQRS7/f1D8AgAA//8DAFBLAQItABQABgAIAAAA IQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0A FAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0A FAAGAAgAAAAhALe+QlJ3CQAAKjUAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsB Ai0AFAAGAAgAAAAhAHuZVKfeAAAACQEAAA8AAAAAAAAAAAAAAAAA0QsAAGRycy9kb3ducmV2Lnht bFBLBQYAAAAABAAEAPMAAADcDAAAAAA= " o:allowincell="f">

x

p(x)

m

Это знакомая нам огибающая уровней шариков в ячейках в опыте Гальтона.

Вершина распределения имеет абсциссу, равную математическому ожиданию x = m.

Кривая имеет ось симметрии.

Площадь, заключённая между кривой и горизонтальной осью равна 1.