РАЗБРОС ЗНАЧЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Знание степени разброса значений случайной величины в ряде случаев так же важно, как и знание её среднего значения. А бывает, и совершенно необходимо.
Например, известна пословица: «Река – в среднем по колено, а корова утонула».
Или другой случай. В больничной палате лежат пятеро тяжело больных. У четырёх температура – 40, лихорадка; а у одного – 20, комнатная, т.е. он умер. Какова будет средняя температура по палате?
Вычисляем среднее арифметическое
(40 + 40 + 40 + 40 + 20) / 5 = 180 / 5 = 36 град.
Средняя по палате температура – нормальная… Но значит ли это, что все здоровы?
Поэтому кроме среднего значения случайной величины важно знать что-то о разбросе её значений.
Причём желательно, чтобы это «что-то» было числом. Для возможности сравнения.
Задумаемся, что в рассмотренном примере можно вычислить такого, что характеризовало бы разброс значений?
Например, можно вычислить отклонения каждого значения от среднего арифметического, а затем найти среднее арифметическое этих отклонений.
Попробуем
( (40-36) + (40-36) + (40-36) + (40-36) + (20-36) ) / 5 = (4 + 4 + 4 + 4 + (–16) ) / 5 = 0.
Не подходит.
Знаки отклонений противоположны, поэтому отклонения взаимно уничтожаются.
Следовательно, надо что-то придумать, чтобы избавиться от знаков.
Первая мысль, которая приходит в голову – это вычислить вначале модули этих отклонений, а уже затем – их среднее арифметическое.
( |40-36| + |40-36| + |40-36| + |40-36| + |20-36| ) / 5 =
= (4 + 4 + 4 + 4 + 16) / 5 = 32 / 5 = 6,4 град.
Вот это уже то что надо. Модуль устраняет чувствительность к направленности отклонения, т.е. учитывается только величина этого отклонения без знака.
Эта способ вычисления весьма нагляден и исторически был предложен первым.
Однако впоследствии оказалось, что при его использовании в более сложных ситуациях возникают математические трудности.
Поэтому в настоящее время и в теории вероятности, и в статистике для большего удобства при вычислении отклонения используется не модуль, а возведение в квадрат, т.е. находится среднее арифметическое квадратов отклонений
( (40-36)2 + (40-36)2 + (40-36)2 + (40-36)2 + (20-36)2 ) / 5 =
= (16 + 16 + 16 + 16 + 256) / 5 = 320 / 5 = 64 град2.
Характеристика разброса значения здесь будет иметь размерность «градус в квадрате». (Почти что квадратный градус)
Чтобы вернуться к обычным, привычным градусам, извлекают корень
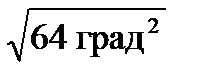 = 8 град.
= 8 град.
Видим, что другой способ вычисления дал другое число. Но и в том, и в другом случае величина характеризует рассеяние или разброс относительно среднего значения.
А теперь давайте серьёзно получим выражение для рассеяния с использованием возведения в квадрат как способа устранения зависимости от знака отклонения.
Рассуждения будут такие же, как и при выводе выражения для среднего арифметического.
Рассмотрим дискретную случайную величину Х (большое) с N возможными значениями.
Пусть с ней проделано n одинаковых опытов.
При этом случайная величина Х значение 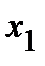 приняла
приняла 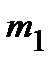 раз,
раз,
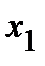 –
– 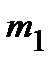 раз
раз
значение 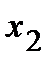 приняла
приняла 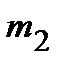 раз,
раз,
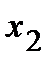 –
– 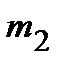
и так далее …,
значение 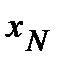 приняла
приняла 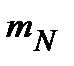 раз
раз
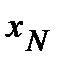 –
– 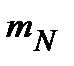 .
.
Общее количество появления всех значений равно n, т.е.
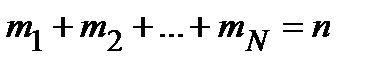
Найдём среднее арифметическое случайной величины Х по n опытам.
Формулу для среднего арифметического уже получали
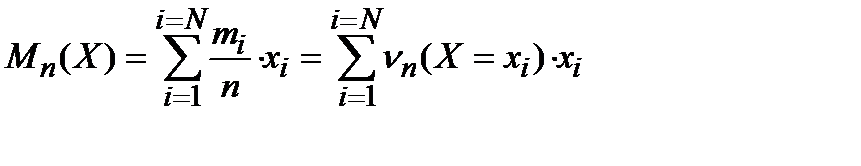 .
.
Теперь займёмся рассеянием.
В примере с больницей мы вычисляли среднее арифметическое квадратов отклонений от среднего. Запишем то же самое в общем виде.
Искомую величину для рассеяния будем обозначать как Dn(X). Рассеяние, по-латински, – дисперсия, т.е. слово начинается на букву «D».
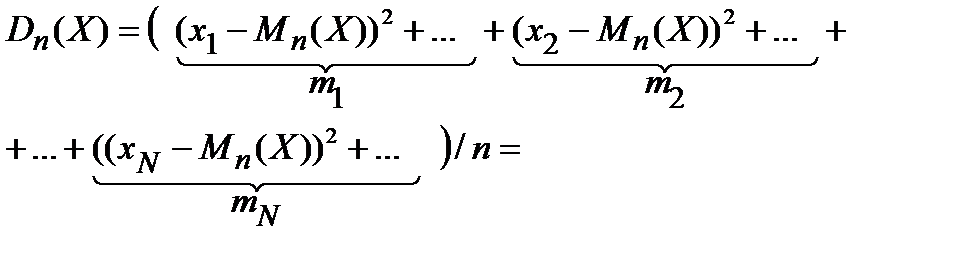
Раскроем внешние скобки и учтём повторяемость значений, т.е., например, то, что 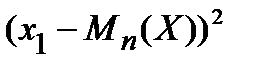 складывается m1 раз, и т.д.:
складывается m1 раз, и т.д.:
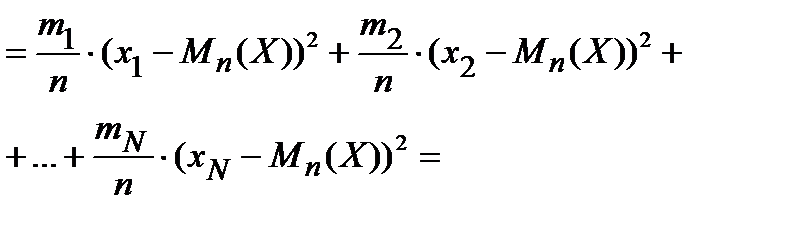
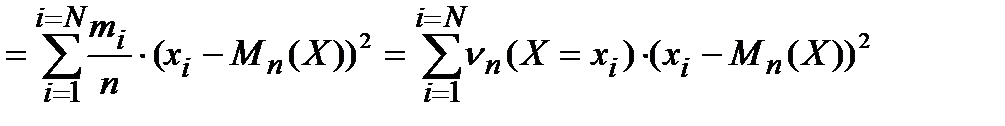
где 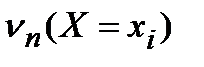 - это частота появления значения
- это частота появления значения 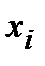 в n опытах.
в n опытах.
Мы вычислили среднее арифметическое квадратов отклонений. Говорят также, что получен средний квадрат отклонения от среднего арифметического.
Из полученного выражения видно, что рассеяние вычисляется как усреднённая сумма квадратов отклонений от среднего арифметического. В качестве множителей при каждом слагаемом суммы выступают частоты 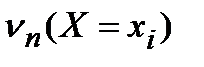 .
.
Дата добавления: 2021-01-26; просмотров: 571;











