ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ
Для удобства дальнейших рассуждений договоримся обозначать случайную величину, которая заранее непредсказуемым образом может принимать различные значения, большой буквой, например, X, а её возможные значения, т.е. числа на оси, одноимённой маленькой, в данном случае: x.
Как мы теперь знаем, закон распределения дискретной случайной величины показывает, насколько одно значение более вероятно, чем другое.
Нужна подобная характеристика и для непрерывной случайной величины.
К сожалению, для непрерывной случайной величины мы не можем опираться на классическое определение вероятности, т.к. количество элементарных исходов бесконечно, а вероятность того, что непрерывная случайная величина X примет какое-либо конкретное значение х0 , исчезающе мала:
P(X=x0) = P(x0) » 0 .
Поэтому прибегнем к «хитрости», которой мы пользовались при рассмотрении доски Гальтона и геометрического определения вероятности.
Наша случайная величина – это координата точки падения шарика на ось.
На оси возможных значений случайной величины X выберем точку х0.
Рассмотрим малый интервал Dx, включающий в себя интересующее значение х0
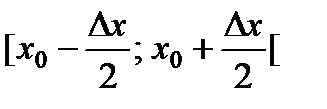 ,
,
а также вероятность попадания в него случайной величины X
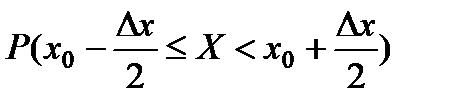
Подробный вывод требует, чтобы слева было нестрогое неравенство, а справа – строгое.
Начнём теперь сокращать протяжённость интервала Dx
Dx ® 0 .
При этом вероятность попадания в него также начнёт уменьшаться, стремясь к нулю
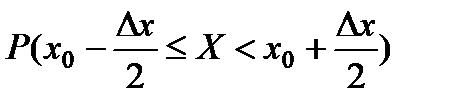 ® 0 .
® 0 .
Рассмотрим отношение этих двух величин
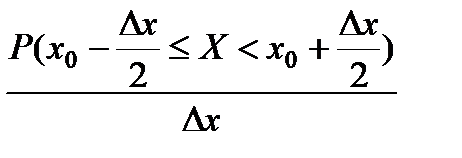 =
=
Несмотря на то, что и числитель, и знаменатель в этой дроби одновременно будут стремиться к нулю, дробь будет стремиться к некоторой ненулевой величине:
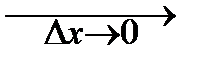 p(x0).
p(x0).
При рассмотрении доски Гальтона мы дали этой величине название: плотность вероятности.
Теперь пришла пора обратить внимание на то, что полученная величина зависит от значения точки х0, поэтому в общем случае она является функцией координаты p(x). Чтобы подчеркнуть это обстоятельство плотность вероятности ещё называют плотностью распределения вероятности или, более кратко, плотностью распределения.
Если попытаться дать развёрнутое определение плотности вероятности, то оно будет звучать так: плотность вероятности численно равна пределу, к которому стремится дробь, в числителе которой – вероятности попадания в отрезок в окрестности рассматриваемой точки, а в знаменателе – длина этого отрезка, при условии, что длина отрезка стремится к нулю.
Полезное свойство плотности распределения p(x) для нас заключается в том, что она позволяет сравнивать вероятности попадания случайной величины в отрезки в окрестности различных точек.
| x |
| p(x) |
| x1 |
| x2 |
Значения случайной величины, имеющие большие значения p(x), более вероятны, чем значения с малыми значениями p(x).
Так на рисунке значение x1 более вероятно, чем x2 , потому что p(x1) > p(x2).
Особая важность функции плотности распределения в том, что она несёт в себе всю информацию о непрерывной случайной величине.
Зададимся вопросом: какова единица измерения функции плотности распределения вероятности, откладываемой по вертикальной оси?
Ответ находим в способе её получения.
Нами рассматривалась дробь, в числителе которой была вероятность, не имеющая размерности, а в знаменателе – длина отрезка по оси x. Если по оси откладывается величина имеющая, например, размерность «метры», то дробь даст размерность «1/метр».
Таким образом, единица измерения плотности вероятности будет обратной по отношению к единице измерения по оси x.
Дата добавления: 2021-01-26; просмотров: 593;











