МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Математическое ожидание непрерывной случайной величины обладает свойством, схожим с тем, которое мы рассмотрели для дискретной:

математическое ожидание непрерывной случайной величины – это абсцисса центра тяжести, но не закона распределения, а плотности распределения.

Т.е. если имеется вырезная, например, из листа железа фигура, описываемая функцией p(x), и для неё вычислено математическое ожидание M(X), то, подвесив эту фигурку за отверстие, проделанное вверху перпендикуляра, поднятого из точки M(X), мы увидим, что эта фигура не покосится набок.

Это и означает, что нами найдена абсцисса центра тяжести этой фигуры.

M(X)

p(x)

центр тяжести

Таким образом, и для непрерывной случайной величины математическое ожидание соответствует абсциссе центра тяжести.

Для полноты изложения материала без вывода и пояснений запишем формулу для вычисления математического ожидания по известной плотности распределения p(x). Правда, обозначения в ней будут понятны только тем, кто со школы помнит, что такое интеграл. Она во многом похожа на формулу для математического ожидания дискретной случайной величины, которую мы недавно вывели.

Итак, математического ожидания дискретной случайной величины:

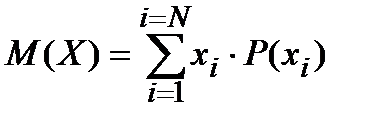
А для непрерывной случайной величины математическое ожидание:

.

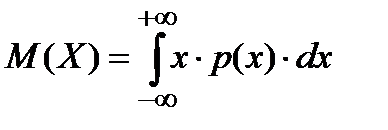S-образный значок интеграла происходит от слова Summa. При интегрировании, в отличии от обычного сложения, производится суммирование бесконечного количества слагаемых. После значка интеграла идёт произведение возможного значения x случайной величины X на вероятность того, что случайная величина X его примет, p(x) × dx (см. последнее свойство плотности распределения). Т.е. то же, что и в случае дискретной случайной величины.

После подстановки в эту формулу функции p(x) и вычисления определённого интеграла получается число, математическое ожидание, которое имеет смысл среднего значения непрерывной случайной величины.

Это число указывает абсциссу центра тяжести фигуры p(x).

Практическое значение математического ожидания.

Состоит в том, что как для дискретных, так и для непрерывных случайных величин может быть рассчитана единая числовая характеристика: математическое ожидание.

Оно позволяет сравнивать любые случайные величины между собой в том, каково их среднее значение.

Мы уже знакомы с двумя видами непрерывных случайных величин: равномерно распределённой и нормально распределённой.

Узнаем, чему у них равны математические ожидания.

Равномерно распределённая случайная величина имеет такую математическую запись плотности вероятности

x

p(x)

b

a

M(X)

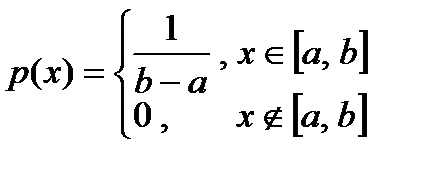
Вычислим математическое ожидание, как это делалось в школе (кто помнит, что такое интеграл, тот поймёт),

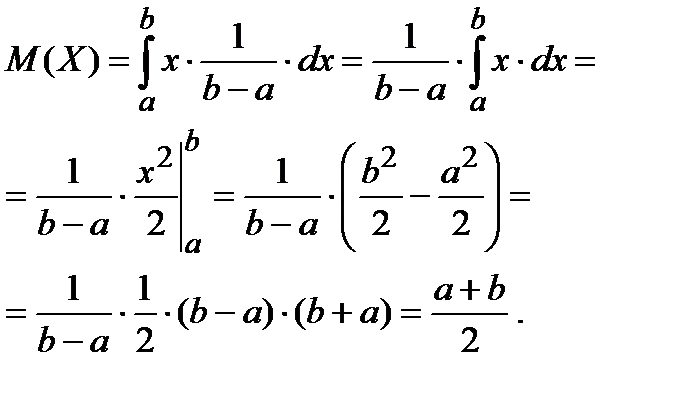
Математическое ожидание совпадает с серединой отрезка [a; b], как и полагается абсциссе центра тяжести.

Нормально распределённая случайная величина имеет следующую плотность вероятности

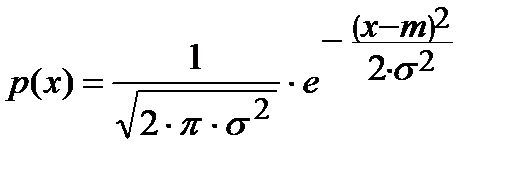
Оказывается, что, несмотря на сложность записи, математическое ожидание совпадает со значением параметра m, который входит в формулу

.

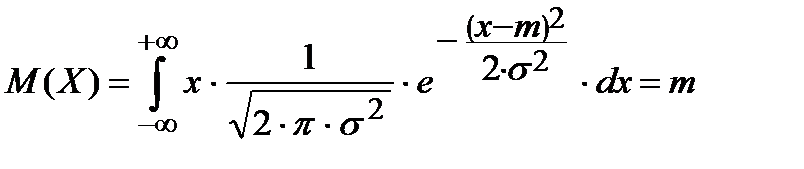Значение m находится на оси x под вершиной кривой.

x

p(x)

m

Бывают и несимметричные распределения, т.е., например, скошенные набок. Для них математическое ожидание с максимумом не совпадает.

x

p(x)

M(X)

Теперь применим наши знания о математическом ожидании для сравнения случайных величин

Случайные величины с распределениями «1» и «2» имеют различное математическое ожидание.

«1»

x

p(x)

m2

m1

«2»

Случайные величины с распределениями «3» и «4» имеют одинаковое математическое ожидание. Но, очевидно, что они различны, т.к. случайная величина «4» имеет меньший разброс.

x

p(x)

m1 = m2

«3»

«4»

Таким образом, при сравнении случайных величин недостаточно ограничиваться сравнением их математических ожиданий.

Очень часто важна ещё и степень рассеяния.

Обобщим, что мы знаем об отличии математического ожидания от среднего арифметического.

Среднее арифметическое – это значение, получаемое в результате обработки эмпирических или опытных данных. Поэтому его ещё называют эмпирическим средним.

Математическое ожидание является вероятностным обобщением среднего арифметического при неограниченном возрастании количества опытов. Но так на практике значение математического ожидания не получают.

Оно находится по закону распределения или плотности распределения с помощью алгебраических действий, т.е. теоретически. Поэтому, его называют теоретическое среднее.

Теперь о том, почему теоретическое среднее называют математическим ожиданием. Возможно, потому, что математическое ожидание – это наиболее вероятное или ожидаемое значение, полученное с помощью математики.