Свойства дисперсии.

1.

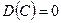
2.

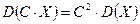
3.

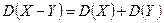
4.

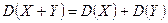
Определение 3. Средним квадратическим отклонением 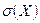случайной величины X называется корень квадратный из её дисперсии:

.

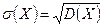Пример. Случайная величина X – число очков, выпавших при однократном бросании игральной кости. Определить .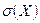

Закон распределения случайной величины X задан таблицей:

Находим математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:

;

;

.

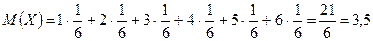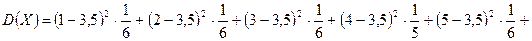
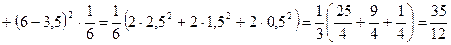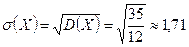Введение среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используется среднее квадратическое отклонение.

Задачи

1. Имеется четыре ящика. В первом ящике 2 белых и 2 чёрных шара, во втором – 3 белых и 4 чёрных шара, в третьем – 3 белых и 8 чёрных шаров, в четвёртом – 6 белых и 7 чёрных шаров. Выбирают наугад один из ящиков и вынимают из него шар. Найти вероятность того, что этот шар белый.

2. Имеется четыре ящика. В первом ящике 3 белых и 3 чёрных шара, во втором – 2 белых и 4 чёрных шара, в третьем – 2 белых и 8 чёрных шаров, в четвёртом – 6 белых и 7 чёрных шаров. Выбирают наугад один из ящиков и вынимают из него шар. Найти вероятность того, что этот шар чёрный.