Свойства функции Лапласа.

1. .

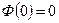Доказательство: .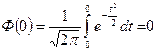

2. Ф(x) – нечётная функция, т.е. Ф(-x)=-Ф(x).

Доказательство:

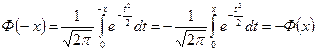(замена t=-z, dt=-dz).

3. Функция Ф(x) монотонно возрастает.

Из формул (2) и (3) следует, что вероятность того, что случайная величина X примет значение из интервала 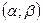равна:

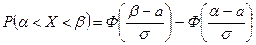. (4)

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 0 и 2. Найти вероятность того, что X примет значение, принадлежащее интервалу (-2;3).

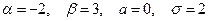. По формуле (4) получаем:

.

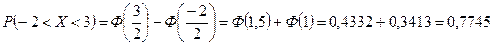Часто требуется вычислить вероятность того, что отклонение нормально распределённой случайной величины X от её математического ожидания по абсолютной величине меньше заданного положительного числа 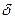, т.е. найти 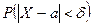. По формуле (4) получаем:

.

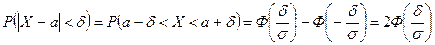Таким образом,

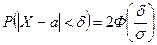. (5)

Пример. Пусть случайная величина X распределена по нормальному закону с параметрами 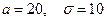. Найти .

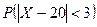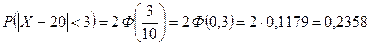
Нормальное распределение вероятностей имеет в теории вероятностей большое значение. В частности, закон распределения суммы достаточно большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, близок к нормальному распределению. Этот факт получил название центральной предельной теоремы.