Свойства функции распределения.
1. 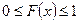 .
.
2. F(x) – неубывающая функция, т.е. если 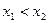 , то
, то 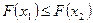 .
.
Доказательство: Пусть 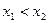 .
.
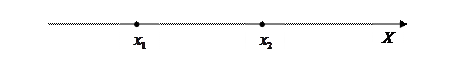
A – событие «X примет значение меньше 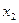 »;
»;
B – событие «X примет значение меньше 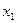 »;
»;
C – событие «X примет значение, удовлетворяющее условию 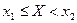 ».
».
Тогда A=B+C, где B и C – несовместны, т.е. P(A)=P(B)+P(C). Таким образом, 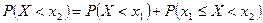 .
.
Отсюда 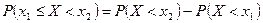 .
.
Так как 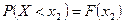 ,
, 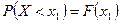 , то
, то 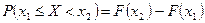 . Поскольку
. Поскольку 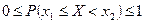 , получаем
, получаем 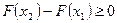 , т.е.
, т.е. 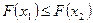 , что и требовалось доказать.
, что и требовалось доказать.
3. Вероятность попадания случайной величины X в полуинтервал 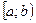 равна разности между значениями функции распределения в правом и левом концах интервала
равна разности между значениями функции распределения в правом и левом концах интервала 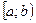 :
:
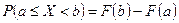 . (2)
. (2)
Пример. Случайная величина X задана функцией распределения:
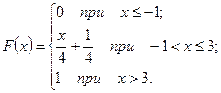
Найти вероятность того, что в результате испытания X примет значение из полуинтервала 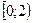 .
.
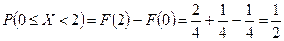
4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
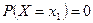 .
.
5. Вероятности попадания непрерывной случайной величины в интервал, отрезок и полуинтервал с одними и теми же концами одинаковы:
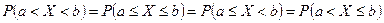 .
.
6. Если возможные значения случайной величины X принадлежат интервалу (a;b), то:
1) F(x)=0 при 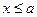 ;
;
2) F(x)=1 при 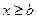 .
.
Следствие. Если возможные значения непрерывной случайной величины X расположены на всей числовой оси, то 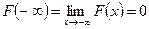 ;
; 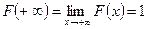 .
.
Дата добавления: 2021-01-26; просмотров: 581;











