Закон нормального (гауссовского) распределения.

Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если её плотность вероятности определяется формулой:

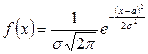, (1)

где .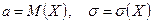

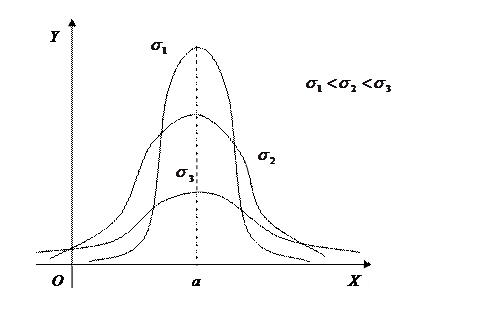
График функции f(x) (кривая Гаусса) имеет следующий вид (точка максимума 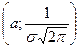), причём его максимальная ордината 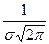убывает с возрастанием значения 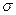(кривая «сжимается» к оси OX) и возрастает с убыванием значения 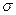(кривая «растягивается» в положительном направлении оси OY). Изменение значения параметра a (при неизменном значении 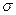) не влияет на форму кривой.

Нормальное распределение с параметрами 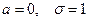называется нормированным. Функция плотности вероятности для такого распределения имеет вид:

.

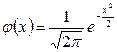Для этой функции составлена таблица её значений для положительных значений x (функция 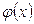чётная). График 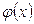имеет следующий вид:

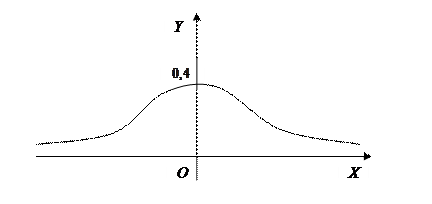
Эту кривую называют единичной нормальной кривой. Она играет роль стандарта, т.е. любые собранные в статистических исследованиях данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой.

Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу 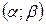равна:

.

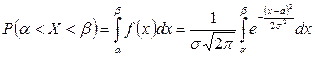Сделаем замену 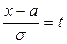, тогда 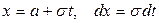, получаем:

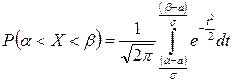. (2)

Интеграл 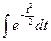не вычисляется в элементарных функциях, поэтому для вычисления интеграла (2) вводится функция

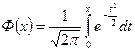, (3)

которая называется функцией Лапласа или интегралом вероятностей. Для функции Лапласа составлена таблица её значений для положительных значений x.