Теорема сложения вероятностей несовместимых событий
Определение 1. Суммой событий A и B называется событие A+B, состоящее в наступлении, по крайней мере, одного из событий A или B.
Аналогично, суммой конечного числа событий 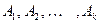 называют событие
называют событие 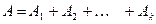 , состоящее в наступлении хотя бы одного из событий
, состоящее в наступлении хотя бы одного из событий 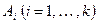 .
.
Определение 2. Произведением событий A и B называется событие C=AB, состоящее в том, что в результате испытания произошло и событие A, и событие B.
Аналогично, произведением конечного числа событий 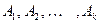 называют событие
называют событие 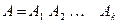 , состоящее в том, что в результате испытания произошли все указанные события.
, состоящее в том, что в результате испытания произошли все указанные события.
Теорема. Вероятность суммы двух несовместимых событий A и B равна сумме вероятностей этих событий.
Доказательство:
Используем классическое определение вероятности. Пусть в данном испытании число всех элементарных событий равно n, событию A благоприятствуют k элементарных событий, событию B – l элементарных событий, событию A+B – k+l элементарных событий (так как события A и B - несовместимые). Тогда по определению вероятности:
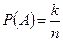 ;
; 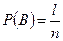 ;
; 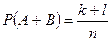 .
.
Следовательно,
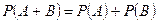 .
.
Теорема доказана.
Следствие. Сумма вероятностей противоположных событий A и 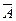 равна единице:
равна единице:
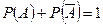 .
.
Доказательство:
События A и 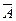 несовместимы. Применим доказанную теорему:
несовместимы. Применим доказанную теорему:
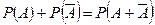 ,
,
но 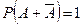 , так как событие
, так как событие 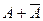 является достоверным (одно из событий A или
является достоверным (одно из событий A или 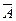 произойдёт). Тогда
произойдёт). Тогда 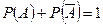 .
.
Пример. На клумбе растут 20 красных, 30 синих и 40 белых астр. Какова вероятность сорвать в темноте окрашенную астру, если срывают одну астру?
A - событие, состоящее в том, что срывают красную астру;
B - событие, состоящее в том, что срывают синюю астру.
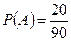 ;
; 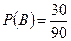 ;
; 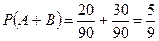
Дата добавления: 2021-01-26; просмотров: 613;











