Нормальное распределение.

Расчет вероятностей по формуле (6) при больших n весьма громоздок. С учетом прерыв­ности величины m аналитическое отыскание суммы вероятностей для областей с некоторыми границами затруднительно [1]. В предельном случае (n→∞, m – любое число, в том числе и не целое, p=0,5) закон биномиального распределения можно выразить иначе. Новое его выражение называется законом нормального распределения (законом гаусса), а плотность вероят­ности в этом случае будет:

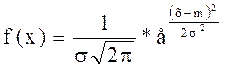, (9)

где т - математическое ожидание величины х; σ - среднее квадратическое отклонение величины х (определение величин m и σ бу­дет дано ниже).

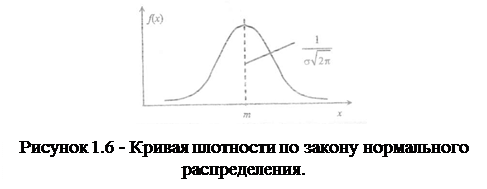
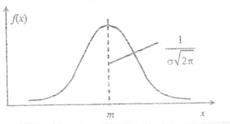
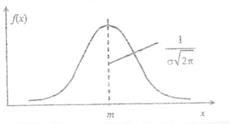
Кривая по закону нормального распределения имеет симметричный вид, при этом максимальная ордината кривой равна 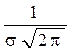в точке х=т; по мере удаления от точки m плотность распределения уменьшается, а при х → ± ∞ кривая асимптотически приближается к оси абс­цисс. Поскольку площадь под кривой плотности в любом случае равна единице, то параметр σ влияет на форму кривой, вытягивая ее вверх при уменьшении значения σ.

Большинство встречающихся на практике случайных величин могут быть представлены как суммы весьма большого числа от­дельных слагаемых, практически не зависящих друг от друга.

На­пример, отклонения в попаданиях снарядов от средней точки при­целивания зависят от метеоусловий, отклонений в массе снаряда и т. д. Показано [1], что такая сумма приближенно подчиняется закону нормального распределения. При этом, чем большее число факторов будет влиять на рассматриваемую случайную величину, тем ближе будет это распределение к теоретическому нормальному закону распределения.

Закон нормального распределения, имеющий глубокое теоре­тическое обоснование его свойств, используется в качестве основ­ного во многих практических исследованиях, результаты опытов сравниваются именно с ним.