Распределение Пуассона
Рассматривая закон биномиального распределения (6), можно задать следующие условия: число опытов n стремится к бесконечности, а вероятность р стремится к нулю, при этом их произведение a = n*р сохраняет постоянное значение. Такое предельное представление биномиального распределения называется распределением Пуассона и может быть выражено, как показывает Е. С. Вентцель [1], формулой:
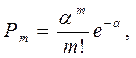 (7)
(7)
позволяющей найти для записанных выше условий вероятность появления некоторого события а при большом числе n независимых опытов, в каждом из которых событие а имеет очень малую вероятность р.
Иногда распределение Пуассона называют законом редких явлений. Покажем его применение на примере. пусть известно, что на ткацком станке нить обрывается в среднем 0,25 раза за один час работы станка (р=0,25). определить вероятность того, что за восемь часов работы произойдет три обрыва нити (т=3).
Для решения определим 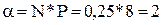 и по формуле (7) получаем искомый результат:
и по формуле (7) получаем искомый результат: 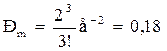
Из формулы (6) можно получить вероятность появления события хотя бы один раз в некоторой группе n:
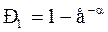 (8)
(8)
Зависимость (8) используют для решения, например, таких задач: определить вероятность поражения малоразмерной цели при стрельбе по площади.
Пусть известно, что цель площадью s=0,6 м2 находится в некотором осколочном поле, характеризующимся двумя попаданиями на один квадратный метр. Если для поражения цели достаточно попадания в нее хотя бы одного осколка, то вероятность такого события при 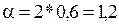 будет равна:
будет равна:
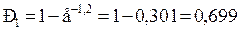
Дата добавления: 2021-01-26; просмотров: 573;











