АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН
Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине.
Случайной величиной называется величина, которая в результате опыта может принять то ли иное значение, причём неизвестно заранее, какое именно. Говоря о значениях случайной величины, мы подчеркиваем тем самым, что они (значения) могут быть получены путём тех или иных измерений. Если ожидаемые результаты измерений можно заранее отделить друг от друга, то соответствующие им случайные величины называются дискретными (число попаданий при пяти выстрелах, количество годных деталей в партии из заранее оговоренного их числа и т.п.). В то же время существуют случайные непрерывные величины, когда возможные их значения не могут быть перечислены, не отделены друг от друга, заполняют непрерывно некоторый промежуток (дальность полёта снаряда, ошибка взвешивания тела на весах и т.п.).
При рассмотрении любой дискретной случайной величины можно установить связь межу конкретным её значением и частотой появления этого значения (в пределе частота событий будет равна вероятности событий). Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями называются законом распределения этой величины.
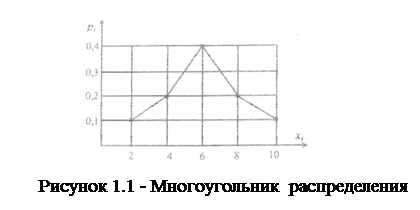
Простейшей формой задания закона распределения является таблица с приведёнными в ней возможными значениями случайной величины хi соответствующими им вероятностями (ряд распределения). Пример такого ряда распределения приведён в табл. 1.1.
Таблица 1.1 - Табличные распределения
| хi | |||||
| pi | 0,1 | 0,2 | 0,4 | 0,2 |
Поскольку дискретные величины являются несовместными, то полная сумма их вероятностей 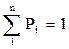 для придания ряду распределения наглядного вида часто изображают его графически, получая многоугольник распределения.
для придания ряду распределения наглядного вида часто изображают его графически, получая многоугольник распределения.
Пример, соответствующий данным, приведенным в табл. 1.1, показан на рис. 1.1.
 |
Ряд распределения дает исчерпывающую характеристику случайной величины, но построить его для непрерывной случайной величины нельзя, так как невозможно перечислить все ее возможные значения для количественной характеристики такого распределения удобно воспользоваться не вероятностью события х=хi а вероятностью события х<хi, и ввести понятие функции распределения, называемой иногда интегральной функцией распределения:
f(xi) = p(x<xi). (1)
Она имеет следующие общие свойства:
1) функция распределения f(хi) есть неубывающая функция своего аргумента;
2) на минус бесконечности функция распределения равна нулю, то есть f(-∞) = 0;
3) на плюс бесконечности функция распределения равна единице, то есть f(+∞) = 1.
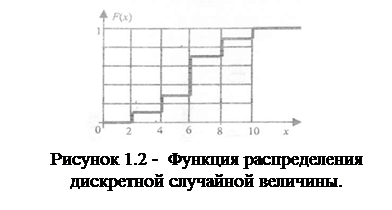
Функция распределения - универсальная характеристика случайной величины. Она существует и для непрерывных, и для дискретных случайных величин. Так, для примера, приведенного в табл. 1.1, график функции распределения показан на рис. 1.2.
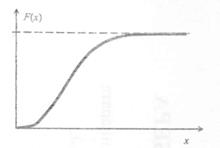
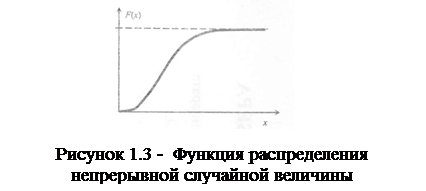
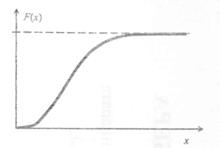
Если на некоторых участках случайная величина будет изменяться непрерывно, то на данных участках f(xi) будет плавно возрастать, если же случайная величина непрерывна на всех участках, го она примет вид кривой, приведенной на рис. 1.3.
|
|
Как следует из определения функции f(x), что и отражено на рис 1.2 и 1.3, функция распределения дискретной величины изображается ступенчатой линией, а функция распределения непрерывной случайной величины в виде плавной возрастающей линии.
Важной характеристикой случайной величины является ее плотность вероятности, или плотность распределения. Так называют предел отношения вероятности попадания значения случайной величины в бесконечно малый интервал (х, х + δх) к длине этого интервала:
δх: 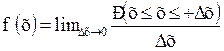 , (2)
, (2)
что, собственно, является производной функции распределения.
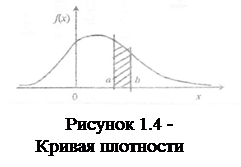
Вид кривой плотности распределения для общего случая показан на рис. 1.4.
 |
Следует отметить, что плотность распределения существует только для непрерывных случайных величин.
Ее основные свойства:
1. Плотность распределения не является отрицательной величиной: f(х) ≥ 0.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
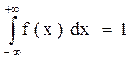 (3)
(3)
3. Вероятность попадания случайной величины х в интервал а, b (см. рис. 1.4) определяется равенством:
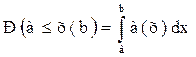 (4)
(4)
4. Функция распределения f(x) может быть выражена через плотность распределения:
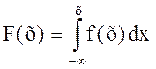 (5)
(5)
Плотность распределения является одной из форм закона распределения. Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона.
Биномиальное распределение – это когда каждый член разложения численно равен вероятности некоторого события а, характерного тем, что при известной вероятности Р его появления в каждом единичном опыте оно появится т раз из возможного числа n всех испытаний. Общий член разложения удобнее представить в виде:
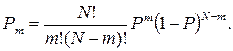 (6)
(6)
Эта формула и представляет собой закон биномиального распределения. Поскольку величины m могут принимать только вполне определенные целые значения, то данное распределение относится только к дискретным случайным величинам. График биномиального распределения представляет собой ломаную линию, форма которой зависит от значений р, т и n. на рис. 1.5;
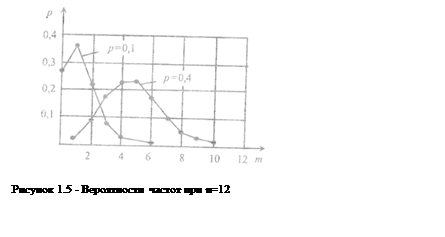 |
Дата добавления: 2021-01-26; просмотров: 742;











