В теории вероятностей и её приложениях нормальное распределение играет особо важную роль.

Решим теперь важную задачу. Пусть случайная величина ξ распределена по нормальному закону с параметрами .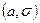

Найдём вероятность попадания величины ξ в произвольный отрезок .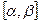

Имеем:

.

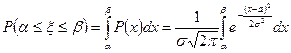Если в последнем интеграле произвести замену 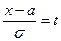, то получим:

,

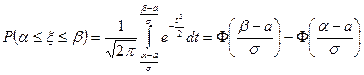где Ф(х) есть функция Лапласа, введенная в §12 гл.1

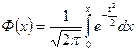. (10)

Таким образом, имеет место формула:

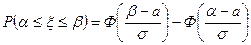, (11),

которая и решает поставленную задачу.

В частности, вероятность попадания в отрезок 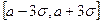будет равна: .

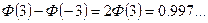Эта вероятность отличается от 1 на весьма малую величину. Отсюда следует, что событие 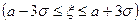является практически достоверным, т.е., что практически возможные значения величины ξ расположены на отрезке .

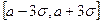Этот факт носит название: правило трёх сигм.

Из формулы (11) нетрудно видеть, что справедлива формула:

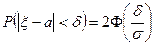. (12)

С помощью этой формулы можно находить вероятность попадания величины ξ на участок, симметричный относительно точки а.

3. Показательное распределение.

Распределение с плотностью 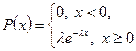называется показательным распределением.

Пользуясь формулой (3) получим, что функция распределения показательного закона имеет вид:

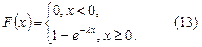
Вероятность попадания в интервал 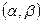случайной величины 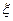, распределённой по показательному закону, будет равна:

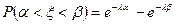. (14)

Пример. Пусть устройство начинает работать в момент времени 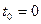, а в момент t происходит отказ.

Часто случайная величина Т-длительность безотказной работы устройства имеет показательное распределение, функция распределения которого:

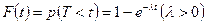(15)

определяет вероятность отказа устройства за время длительности t.

Функцией надёжности 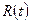называют функцию, определяющую вероятность безотказной работы устройства за время длительности t:

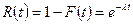. (16)

Параметр λ в формулах (15) и (16) равен интенсивности отказов (среднее число отказов в единицу времени).