Вычисление средних величин.
Одной из основных характеристик случайной величины является ее математическое ожидание:
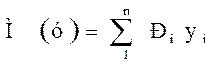 (10)
(10)
где pi - вероятность появления случайной величины у, в каждом п, измерении при их общем числе n.
При ограниченном числе измерений вместо вероятности используется частота события и вместо м(у) определяется средняя арифметическая величины у:
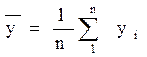 (11)
(11)
Для измерений, подчиняющихся закону нормального распределения, иногда вместо средней арифметической величины используют моду (наиболее часто встречающуюся величину) или медиану (среднюю в ранжированном ряду величин).
Конкретные величины уi будут отличаться от средней на разность 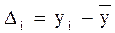 .
.
Для анализа этих отклонений используются следующие характеристики:
1) среднее арифметическое отклонение
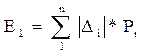 (12)
(12)
А для малого числа измерений
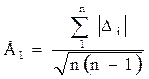 (13)
(13)
2) среднее квадратическое отклонение
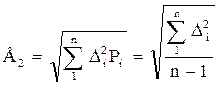 (14)
(14)
При этом, 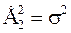 -дисперсия (математическое ожидание квадрата отклонения случайной величины от ее математического ожидания).
-дисперсия (математическое ожидание квадрата отклонения случайной величины от ее математического ожидания).
В дальнейшем мы будем обозначать дисперсию 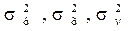 и т. п., подчеркивая, какую конкретно величину мы анализируем;
и т. п., подчеркивая, какую конкретно величину мы анализируем;
3) срединное (вероятное отклонение) е - это такая величина, относительно которой вероятность отклонений в большую и меньшую сторону одинакова и равна 0,5. Соотношения между этими отклонениями приблизительно равны:
6е ≈ 5е1 ≈4е2 (15)
Чаще других используется среднее квадратическое отклонение σу, определяющее характер разброса случайной величины, точность ее определения. Для оценки достоверности полученных результатов А. К. Митропольский [1] рекомендует использовать показатель точности исследования:
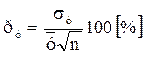 (16)
(16)
Чем точнее проведено исследование, тем меньше будет показатель рт для технических задач его желательно иметь менее 5 %.
Если известна (или задана) мера изменчивости 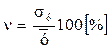 , то из формулы (16) можно получить необходимое для достоверности
, то из формулы (16) можно получить необходимое для достоверности
число экспериментов (наблюдений) n.
При прогнозировании следует знать не только конкретную
среднюю в какой-либо точке ti но и ее изменение от времени или
изменения какого-то иного фактора, то есть знать эти средние в нескольких точках.
Если линии, соединяющие указанные точки,
представляют собой ломаную, то ее следует сгладить. В ряде случаев сглаживание может облегчить применение методов выделения существующих тенденций
изменения y(t).
Один из наиболее простых приемов сглаживания [1] заключается в расчете скользящих средних, позволяющих сделать
плавными периодические и случайные колебания исследуемой величины.
Если рассматривать динамический ряд, состоящий из p уров-
ней, то скользящая средняя будет представлять собой среднюю ве-
личину для т последовательных уровней этого ряда (т < п). Для
каждого i-го уровня ряда скользящая средняя может быть вычисле-
на по формуле:
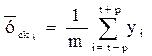 , (17)
, (17)
где 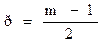
Желательно принимать m нечетным числом, тогда р = 1; 2; 3;...
Как видно, при вычислении скользящей средней теряются 1, 2, 3... Крайние точки ряда. Зато можно наглядно наблюдать существующую тенденцию изменения y(t) (рис. 1.7).
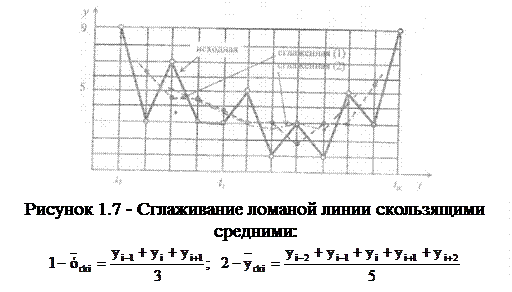
Считая, что простые скользящие средние являются весьма грубым статистическим приемом выявления тенденции, часто искажающим оценку исследуемого процесса, Е.М. Четыркин [3] рекомендует применять взвешенные скользящие средние. Под весом в
В данном случае понимается расстояние от середины интервала сглаживания. Точкам, находящимся ближе к середине конкретного интервала, приписывается больший вес. Метод определения весов, рекомендованный им, позволяет получить следующие формулы для нечетных m:
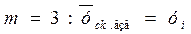 (18)
(18)
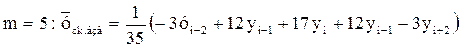 (19)
(19)
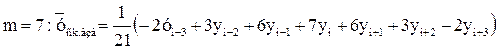 (20)
(20)
Если полученные расчетные значения 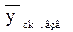 все еще обладают значительной колеблемостью, то рекомендуется повторить процесс усреднения, то есть произвести второе, а потом, может быть, и третье сглаживание.
все еще обладают значительной колеблемостью, то рекомендуется повторить процесс усреднения, то есть произвести второе, а потом, может быть, и третье сглаживание.
На наш взгляд, целесообразнее использовать в качестве коэффициентов при у известные биномиальные коэффициенты из так называемого треугольника паскаля. Тогда при нечетных m получатся следующие формулы:
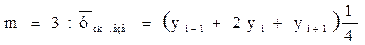 (21)
(21)
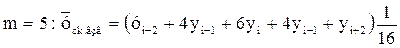 (22)
(22)
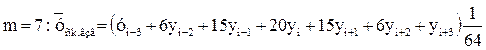 (23)
(23)
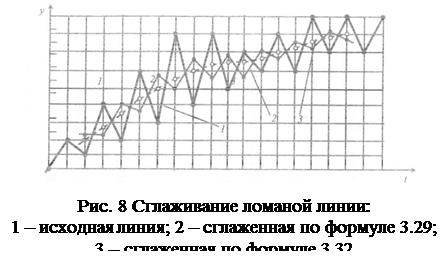
Сглаживания но этим формулам меньше искажают общую тенденцию, а мелкие волны не меняют свой знак (вместо выпуклого участка на кривой не получается вогнутый) для наглядности покажем это на рис. 1.8.
Кстати, для приведенного на рис. 1.8 примера вычисления, произведенные по формуле (19) практически совпадают с вычислениями по формуле (17) при m-3. Также близки между собой вычисления, произведенные по формулам (21) и (22). В связи с этим не всегда нужно расширять интервал сглаживания m.
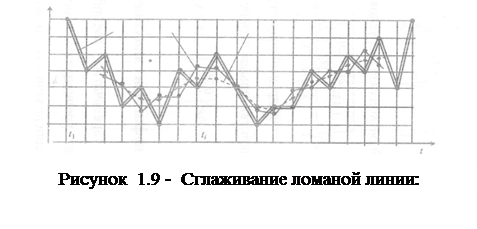
Более мягкое сглаживание по формуле (22), получается также и для ломаной с некоторой цикличностью. Пример этого показан на рис. 1.9.
Следует отметить, что сам термин "взвешенная скользящая средняя" в приведенном выше варианте соответствует одинаковому числу измерений в каждой точке ti. Более логично было бы учесть также число измерений для каждой i-й точки, особенно для технических задач. Для этого каждую величину 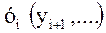 следует умножить на соответствующее число измерений
следует умножить на соответствующее число измерений 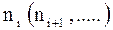 .
.
Результаты измерений 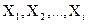 представляют собой случайные величины. Процесс обработки экспериментальных данных заключается в нахождении наивероятнейшего значения измеряемой величины (среднего арифметического
представляют собой случайные величины. Процесс обработки экспериментальных данных заключается в нахождении наивероятнейшего значения измеряемой величины (среднего арифметического 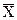 ), точности полученных результатов, средней квадратической и наибольшей возможной ошибки среднего арифметического.
), точности полученных результатов, средней квадратической и наибольшей возможной ошибки среднего арифметического.
Точность отдельного измерения определяется по формуле:
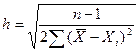
Точности среднего арифметического определяется по формуле:
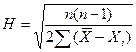 ,
,
т.е. точность среднего арифметического больше точности отдельных измерений и пропорциональна квадратному корню из числа измерений. Cредняя квадратическая ошибка 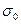 среднего арифметического определяется по формуле:
среднего арифметического определяется по формуле:
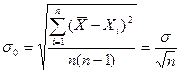 ,
,
где 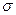 - средняя квадратическая ошибка отдельного измерения.
- средняя квадратическая ошибка отдельного измерения.
Вероятная и наибольшая возможная (при Р-0,997) ошибки среднего арифметического, соответственно, равны:
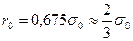 и
и 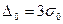
При записи среднего арифметического принято указывать его среднюю квадратическую ошибку.
Дата добавления: 2021-01-26; просмотров: 621;











