Логарифмически нормальное распределение

Случайная переменная Y имеет логарифмически нормальное распределение с параметрами μ и σ, если случайная переменная X = lnY имеет нормальное распределение с теми же параметрами μ и σ. Зная характер связи между переменными X и Y, можем легко построить график плотности вероятности случайной переменной с логарифмически нормальным распределением (Рисунок 4.2).

Рисунок 4.2 – Кривые плотности логарифмически нормального распределения при различных значениях параметров μ и σ

Если случайная переменная X имеет функцию плотности вероятности, определяемую формулой (4.6), и если X = lnY, то:

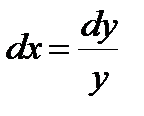, откуда имеем для у > 0:

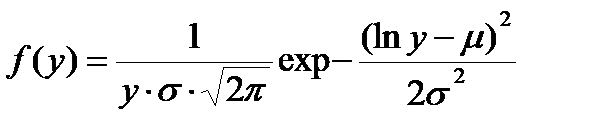(4.14)

Из определения следует, что случайная переменная, подчиняющаяся логарифмически нормальному распределению, может принимать только положительные значения. Как показано на рисунке 4.2, кривые функции f(y) имеют левостороннюю асимметрию, которая тем сильнее, чем больше значения параметров μ и σ. Каждая кривая имеет один максимум и является определенной для всех положительных значений у.

Вычисление математического ожидания и дисперсии случайной переменной с логарифмически нормальным распределением не составляет особых трудностей:

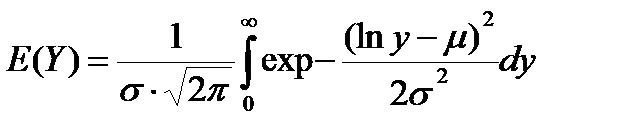(4.15)

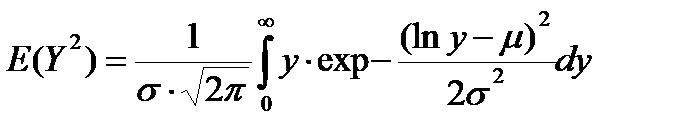(4.16)

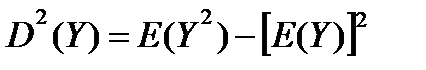(4.17)

Путем подстановок и ввода новых переменных в интегралах 4.15 и 4.16 получим:

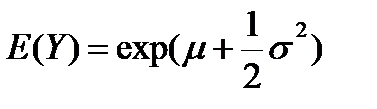(4.18)

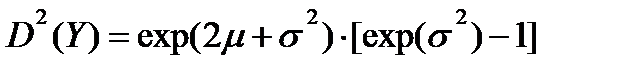(4.19)

Вообще, для исчисления вероятности того, что случайная переменная Y с логарифмически нормальным распределением и плотностью f(y, μ, σ), примет значение в интервале (а, b), следует взять интеграл:

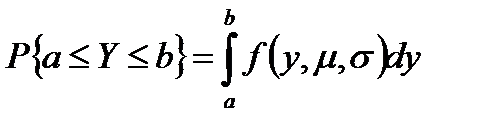(4.20)

Однако на практике удобнее воспользоваться тем, что логарифм случайной переменной Y имеет нормальное распределение. Вероятность того, что а ≤ Y ≤ b равнозначна вероятности того, что
lnа ≤ lnY ≤ lnb.

Пример

Вычислим вероятность того, что случайная переменная с логарифмически распределением μ = 1, σ = 0,5, примет значение в интервале (2, 5). Имеем:

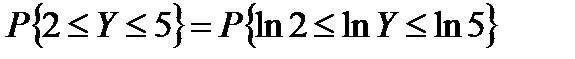
Из таблиц логарифмов находим ln2 = 0,6932 и ln5 = 1,6094.

Обозначив lnY = X, можем написать:

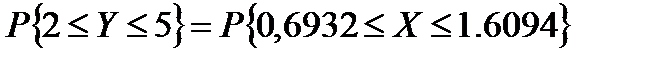
Причем случайная переменная X подчинена нормальному распределению со средним значением μ = 1 и стандартным отклонением σ = 0,5. Теперь искомую вероятность нетрудно вычислить по таблицам интегральной функции нормального распределения:

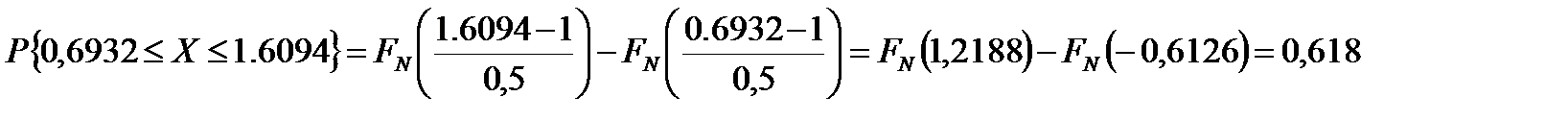
Вопросы для самоконтроля

1 Определение прямоугольного распределения.

2 График плотности вероятности случайной переменной с прямоугольным распределением

3 Основополагающее значение прямоугольного распределения.

4 Математическое ожидание и дисперсия случайной переменной в прямоугольном распределении.

5 Роль нормального распределения в математической статистике.

6 Что такое нормальное распределение и как оно связано с биномиальным?

7 График плотности вероятности случайной переменной с нормальным распределением.

8 Какими статистическими параметрами может быть задано нормальное распределение?

9 Почему нормальное распределение является непрерывным?

10 Уравнение нормальной кривой.

11 Что такое нормированное отклонение?

12 Уравнение кривой нормального распределения в нормированной форме.

13 Какими значениями μ и σ характеризуется нормальная совокупность в нормированной форме?

14 Какая доля данных выборки укладывается в пределах ±1σ, ±2σ, ±3σ?

15 Что показывает таблица нормального интеграла вероятностей?

16 Уравнение логарифмически нормальной кривой.

17 График плотности вероятности случайной переменной с логарифмически нормальным распределением.

18 Какие необходимо выполнить преобразования, чтобы из логарифмически нормального распределения получить нормальное распределение?

19 Какими статистическими параметрами задается логарифмически нормальное распределение?

ТЕМА 5 Распределения параметров выборки

5.1 t – распределение Стьюдента

5.2 F-распределение Фишера–Снедекора

5.3 χ²–распределение