ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Вспомним логическую последовательность при знакомстве с нормальным распределением.

Опыт Френсиса Гальтона

Dx

nn = m/n

x

x

p(x)

N(m;s2)

Воронка с шариками

препятствия

ячейки

Гистограмма

Нормальное распределение

В результате опыта может быть построена столбиковая диаграмма частот попадания в различные ячейки

n_n = m / n.

Dx – ширина ячейки

При неограниченном увеличении числа опытов, то есть

n ®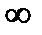

частота стремится к вероятности падания шариков в ячейку P.

При стремлении ширины ячейки к нулю, то есть

Dx ® 0

отношение значения вероятности к ширине ячейки даёт нам плотность вероятности, и появляется колоколообразная кривая плотности распределения вероятности. Она известна нам как нормальное распределение и обозначается как N(m;s²) .

Этот опыт плоский. Он так и называется: доска Гальтона.

Поставим мысленно опыт, подобный доске Гальтона, но не над осью x с ячейками, а над плоскостью x и y, также разбитую на ячейки (как соты в улье).

Также будем бросать шарики и подсчитывать частоту попадания для каждой ячейки.

Координата x и координата y точки падения шарика для нас – случайные величины Х и Y. При данных условиях опыта обе эти случайные величины имеют нормальное распределение.

Далее делаем такой же логический переход.

Частота попадания шарика в какую-либо прямоугольную ячейку размерами Dx и Dy

n_n = m / n.

При неограниченном увеличении числа опытов, т.е. при

n ®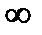

частота стремится к вероятности падания шариков в рассматриваемую ячейку P.

Рассмотрим отношение этой вероятности P к площади ячейки

.

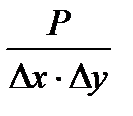При стягивании сторон ячейки к её центру, т.е. при уменьшении размеров ячейки,

Dx ® 0, Dy ® 0,

вероятность попадания в эту ячейку тоже будет стремиться к нулю

P ® 0 .

Но их отношение будет стремиться к некоторой ненулевой величине, описывающей вероятность падания шариков в точку вблизи центра данной ячейки. Это плотность вероятности.

В каждой точке плоскости внизу эта величина будет иметь своё значение p( x, y ).

Полное её название – двумерная (совместная) плотность распределения случайных величин Х и Y. Она имеет вид объёмного колокола или холма.

x

x

y

y

p(x,y)

Воронка с шариками

Препятствия

Ящик с ячейками

Нормальное распределение

Dy

Dx

Поскольку обе они имеют нормальное распределение, получившаяся плотность вероятности – это так называемое двумерное нормальное распределение.

Объём, заключённый между горизонтальной плоскостью и поверхностью этой функции, равен единице. Как в одномерном распределении площадь.

Формулу для двумерного нормального распределения мы записывать не будем, она довольно громоздка.

Но в этой формуле отражается то, что двумерная плотность нормального распределения является функцией двух переменных: координат x и y, а также пяти параметров, т.е. величин, которые входят в выражение в явном виде

p( x, y ) = N₂( m_X, m_Y, s_X², s_Y², r )

Параметры двумерного нормального распределения таковы:

m_X, m_Y – они определяют координаты максимума «колокола»,

s_X², s_Y² – они определяют растяжение по каждой оси,

есть также пятый параметр

r – он называется, коэффициент корреляции.

Для того чтобы понять, как влияют на форму «холма» указанные параметры, изобразим горизонтальные сочетания колоколообразной поверхности двумерного нормального распределения при различных значениях коэффициента корреляции.

Совокупность сечений будет напоминать изображение холма на географической карте.

x

y

mY

mX

Случай 1.

m_X > m_Y .

s_X² > s_Y² .

r = 0 .

Сечения являются эллипсами.

Случай 2.

r > 0 .

x

y

mY

mX

Эллипс наклонён и располагается вдоль возрастающей прямой

y = a× x + b, где a > 0.

x

y

mY

mX

Случай 3.

r < 0 .

Эллипс располагается вдоль убывающей прямой

y = a× x + b, где a < 0.

Как можно увидеть из приведённых примеров, коэффициент корреляции имеет тот же знак, что и угловой коэффициент прямой a.

Однако его величина не равна тангенсу угла наклона.

Коэффициент корреляции может принимать значения только от –1 до +1.

Связь между коэффициентом корреляции и тангенсом угла наклона большей оси эллипса такова

a = tga =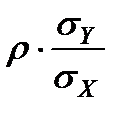

Если вероятностной или статистической связи нет, то эллипс не имеет наклона.

О силе линейной статистической связи судят по двум признакам

1) по наличию наклона эллипса,

2) по степени его вытянутости.

Эти два признака не равноценны. Первый признак более важен. Если есть корреляция, то обязательно есть наклон. Если наклона нет, то нет и корреляции.

О силе корреляции, если она есть, судят по степени вытянутости эллипса.

В случае сильной линейной статистической связи эллипс наклонён и сжат в линию.