Логарифмически-нормальное распределение

Случайная величина 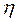называется логарифмически-нормальной, если её натуральный логарифм подчинён нормальному закону распределения.

При этом в отличие от схемы формирования механизма нормального закона последовательный характер воздействия случайных факторов таков, что случайный прирост пропорционален уже достигнутому к данному моменту значению исследуемой величины, т.е. носит не аддитивный, а мультипликативный характер. Пусть 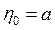- неслучайная компонента исследуемого признака, т.е. «истинное» значение 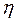, когда нет влияния случайных факторов. Через 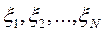обозначим численное выражение эффектов воздействия случайных факторов. Тогда значения случайной величины 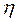, последовательно трансформируемые действием этих факторов будут находиться по формулам

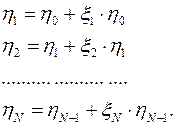
Отсюда легко получить

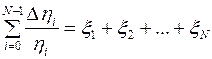(1)

где 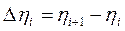. Но правая часть в формуле (1) есть результат аддитивного действия множества случайных факторов, что при сделанных выше предположениях может приводить к нормальному распределению этой суммы. Предполагая относительную незначительность воздействия каждого случайного фактора, т.е. пологая 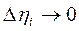, можно в левой части перейти к интегралу

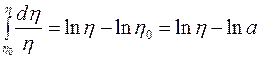
Это и означает, что логарифм интересующей нас величины подчиняется нормальному закону с нулевым средним значением. Функция распределения случайной величины 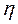имеет вид

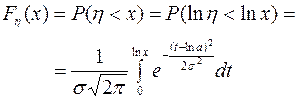
Соответственно функция плотности равна

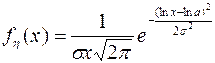
Описанная схема формирования значений логарифмически-нормальной случайной величины характерна для многих физических и социально-экономических ситуаций (размеры и вес частиц, образующихся при дроблении; заработная плата работника; доход семьи; размеры космических образований; долговечность изделия и др.).