Постпроцессорная обработка управляющего сигнала

Очевидно, что уместно масштабирование выхода, полученного в результате дефаззификации. В случае использования стандартного универсума для выхода возникает необходимость преобразования выхода к величине, имеющей инженерную (физическую) размерность, например, вольт, метр, тонна или тонна в час. Примером может служить преобразование стандартного универсума [-1,1] в физические единицы [-10,10] вольт.

Блок конечной обработки сигнала (постпроцессор) часто содержит усилитель с подлежащим настройке коэффициентом усиления и иногда интегратор.

Пример 2.3 (инференция). Каким образом осуществлена инференция на рис. 2.10 при использовании дискретных универсумов?

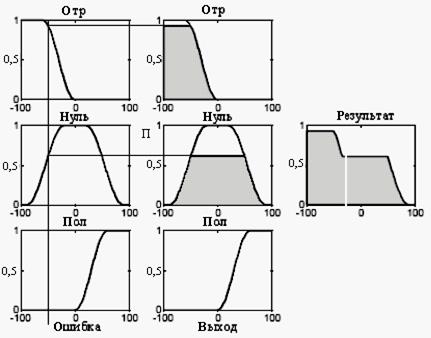
Рис. 2.10

Фактически все универсумы 100,100] были разделены на равные части 201–й точкой.

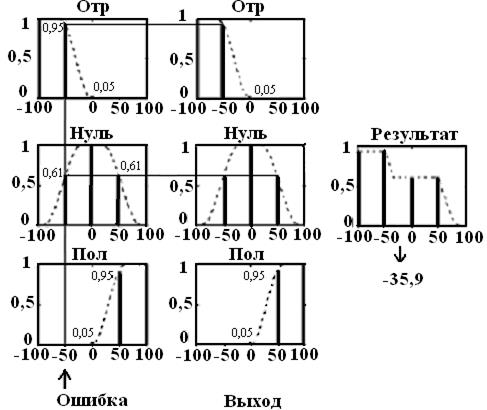
Рис. 2.11

Однако для простоты разделим универсумы ошибки и выхода (управления), используя пять точек (рис. 2.11). При этом универсум u, общий для всех переменных, является вектором

Терм – множества для ошибки и выхода определяются с помощью - функции, описываемой согласно (1.5) как

,

так что

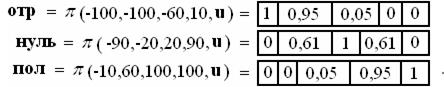
Выше мы ввели вектор u вместо текущей точки x; в результате имеем вектор для каждого терма.

На рис. 2.11 предполагается, что ошибка равна -50 (единица измерения представляет собой процент от полного диапазона ошибки). Это значение соответствует второму элементу универсума и, следовательно, первое правило вносит вклад со степенью принадлежности 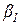= отр(2) =0,95. Эта степень истинности воздействует на правую часть правила с использованием

Рис. 2.11

операции min,так что нечеткий логический вывод для первого правила выглядит так

.

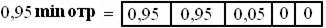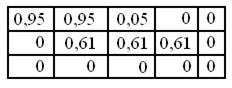
Как видим, для активизации здесь использована операция min. Применяя ту же процедуру для двух оставшихся правил, для которых 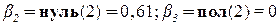, и располагая три нечетких логических вывода в колонку один за другим, получаем таблицу

.

Чтобы найти аккумулированный логический вывод, применим оператор max к каждому столбцу таблицы. В результате получим вектор

,

представляющий собой результирующую дискретную функцию принадлежности выхода, соответствующую входу -50 (см. результат на рис. 2.11) . Метод центра тяжести (2.33) дает следующий результат

=

=

,

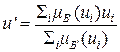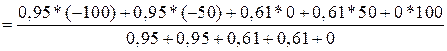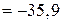который является управляющим сигналом (перед конечной обработкой). Визуализация всех этапов инференции иллюстрируется на рис. 2.11.