Метод центра тяжести для синглтонов (одноточечных множеств)(COGS)

Специальный случай лингвистической модели получается, когда нечеткие множества B_i заключений (выхода), в данном случае управляющего сигнала являются синглтонами (одноточечными множествами). Такие множества представляют собой просто вещественные числа s_i ,что приводит к следующим правилам

Если x₁ есть A_1i и x₂ есть A_2i и … x_r есть A_ri , то u есть s_i, .

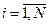Эта модель называется синглтонной моделью. Более простая версия формулы (2.33) (метод нечетких средних) обычно используется для определения четкого выхода такой модели:

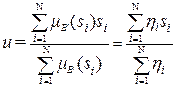. (2.35)

Здесь 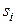позиция i-го синглтона в универсуме выхода, 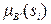равно возбуждающей силе 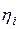i-го синглтона, N- число правил. По формуле (2.35) для рассмотренного в на рис. 2.8 примера было вычислено четкое значение управляющего сигнала, равное -60,5. Оно представлено синглтоном в виде тонкой вертикальной линии на рис.2.8 (крайний нижний ряд справа).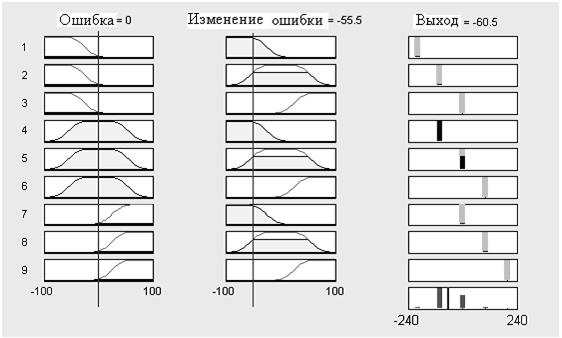

Этот метод дефаззификации относительно предпочтителен с точки зрения вычислительной сложности и к тому же u − функция, дифференцируемая в отношении синглтонов 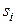, что благоприятно с точки зрения его (метода) использования в нейронечетких системах (см. ниже).

Заметим, что синглтонная нечеткая модель принадлежит к общему классу аппроксимирующих функций (аппроксиматоров), называемых разложением на базисные функции и имеющих вид

.

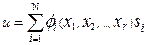Большинство структур, используемых для идентификации нелинейных систем, таких, как искусственные нейронные сети, нейронные сети с радиальными базисными функциями или сплайны принадлежат к этому классу аппроксиматоров. В синглтонной модели для r входов базисными функциями 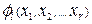являются нормализованные степени истинности (возбуждающие силы) правил

,

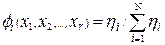и постоянными 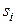являются заключения (синглтоны) правил.

Теорема об универсальной аппроксимации.

Используя теорему Стона-Вейерштрассса, Ванг (1992) показал, что нечеткая логическая модель в форме

Если x есть Ai и y есть Bi,то z есть Ci, i = 1, . . . , n

• сгауссовскими функциями принадлежности

, , ,

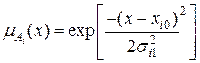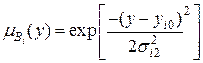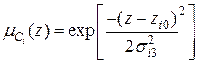• синглтонной фаззификацие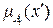й

и ,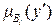

• нечеткой конъюнкцией в виде алгебраического произведения

,

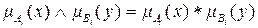• нечеткой импликацией в виде алгебраического произведения

,

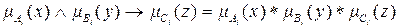• дефаззификацией в форме центра тяжести

,

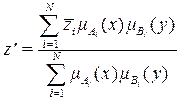где 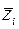является центром (ядром) ФП 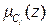, представляют собой универсальные аппроксиматоры, т.е. они могут аппроксимировать любую функцию на компактном (замкнутом) множестве с произвольной точностью, а именно, он доказал следующую теорему.

Теорема. Для данной вещественно значимой непрерывной функции g на компактном (замкнутом) множестве U и заданном произвольном 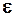>0, существует нечеткая логическая модель с выходом f таким, что

.

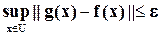Опустить

Биссектриса площади (BOA). В этом методе u = 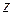, где значение 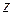определяется из уравнения

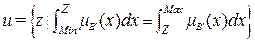. (2.36)

Из (2.36) следует, что uравняется абсциссе вертикальной линии, которая делит площадь под кривой 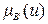выходной переменной на две равные части. В (2.36) x − текущее значение точки в универсуме, 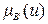− функция принадлежности выхода, Min − левое крайнее значение универсума, Max − правое крайнее значение универсума. Вычислительная сложность этого метода относительно высока, и, кроме того, он может породить сомнения, касающиеся конечного результата. Например тогда, когда нечеткое множество выхода содержит два синглтона с равными степенями истинности, симметрично расположенных относительно нулевого значения. Отсюда можно сделать вывод, что в дискретном случае этот метод применять нельзя.

Метод среднего максимума (MOM). Интуитивный подход − выбрать управление, которое соответствует максимальному значению степени принадлежности выхода, т.е. выбрать наиболее правдоподобное управление. Может случиться, что существует несколько таких максимумов и общий подход − выбрать среднее из значений выхода, соответствующих этим максимумам. Такой метод игнорирует форму функции принадлежности выхода, но обладает относительно невысокой сложностью.

Метод левого максимального значения (LM) и метод максимального правого значения (RM). Другая возможность − выбрать управление, соответствующее крайнему левому максимуму (LM) или крайнему правому (RM) максимуму функции принадлежности выходной переменной. В случае когда объектом управления является робот, он должен выбрать между направлениями движения налево или направо, чтобы избежать столкновения с препятствием, находящимся перед ним. При этом дефаззификатор должен выбрать одно из этих направлений, но ни в коем случае не направление между ними.

Читать