Алгоритм разложения сигнала по неортогональному базису
При обработке экспериментальных функций времени может возникнуть необходимость представления этих функций в виде аналитических выражений. Непрерывный процесс f(t), определенный на интервале T, можно разложить по заранее выбранной системе базисных функций ф1(t)…фn(t), где n – число базисных функций. Разложение S(t) имеет вид:
S(t) = 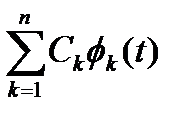 ; f(t) = S(t) + d(t) (1.1) Здесь d(t) = f(t) – S(t) (1.2)
; f(t) = S(t) + d(t) (1.1) Здесь d(t) = f(t) – S(t) (1.2)
-ошибка разложения
Введем понятие энергии Ey функции (сигнала) y(t):
Ey = 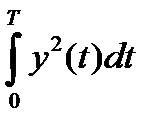 (1.3)
(1.3)
В качестве критерия, характеризующего удаление S(t) от f(t) на интервале T, то-есть характеризующего качество разложения, примем энергию ошибки
Ed = 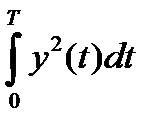 (1.4)При заданных f(t) , T и фi(t) энергия ошибки является функцией от коэффициентов Ci разложения. Коэффициенты разложения будем выбирать из условия минимума энергии ошибки, для чего приравняем нулю частные производные
(1.4)При заданных f(t) , T и фi(t) энергия ошибки является функцией от коэффициентов Ci разложения. Коэффициенты разложения будем выбирать из условия минимума энергии ошибки, для чего приравняем нулю частные производные
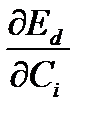 = 0 ; i = 1…n . (1.5)
= 0 ; i = 1…n . (1.5)
Из (4) и (2) можно получить:
Ed = 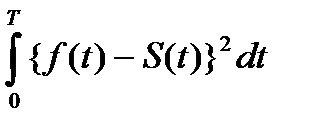 = Ef – A + Es ; (1.6)
= Ef – A + Es ; (1.6)
Ef = 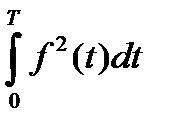 , A = -2
, A = -2 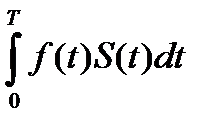 , Es =
, Es = 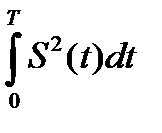
С учетом (6) уравнения (5) станут:
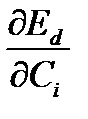 =
= 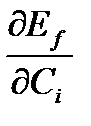 -
- 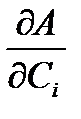 +
+ 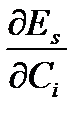 = 0; i = 1…n (1.7)
= 0; i = 1…n (1.7)
Используя (1) и (6) , выпишем частные производные:
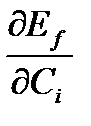 = 0;
= 0; 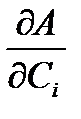 = 2
= 2 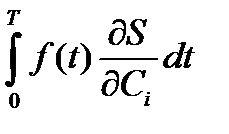 (1.8)
(1.8)
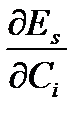 = 2
= 2 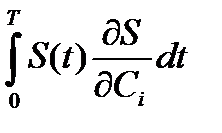 ;
; 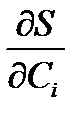 = фi (t)
= фi (t)
Подставив (8) в (7), получим:
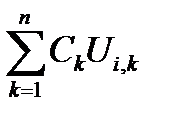 = Vi; i = 1…n . (1.9)
= Vi; i = 1…n . (1.9)
Здесь введены обозначения:
Ui,k = 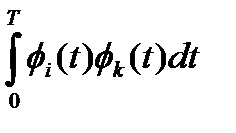 ; Vi =
; Vi = 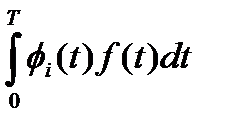 . (1.10)
. (1.10)
Линейная алгебраическая неоднородная система уравнений (9) вместе с обозначениями (10) определяет значения коэффициентов разложения Ci , при которых энергия Ed ошибки разложения минимальна. Используя обозначения (10), энергию ошибки (4) при произвольных значениях коэффициентов Ci можно представить:
Ed = Ef – 2 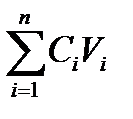 +
+ 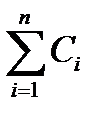
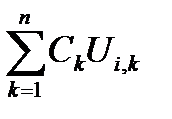 . (1.11)
. (1.11)
При оптимальных значениях коэффициентов, вычисленных из (9), энергия ошибки (11) имеет вид:
Ed = Ef - 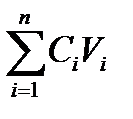 = Ef –Es . (1.12)
= Ef –Es . (1.12)
Приведенные выше результаты имеют достаточно прозрачное геометрическое представление. Введем в рассмотрение пространство H (бесконечномерное), элементами которого являются функции, определенные на интервале T, и удовлетворяющие условиям Дирихле, то – есть ограниченные и имеющие конечное число экстремумов и разрывов первого рода. Любая такая функция представляется в пространстве H точкой или, что эквивалентно, вектором. Определим скалярное произведение двух векторов в пространстве H следующим образом:
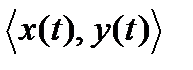 =
= 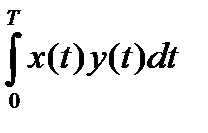 (1.13)
(1.13)
Пространства, в которых определена операция скалярного произведения, называются Гильбертовыми. Они обладают геометрическими аналогиями, вследствие которых суждения, полученные из геометрического рассмотрения, имеют силу доказательств. Квадрат модуля любого сигнала y(t) в пространстве H равен энергии этого сигнала, что видно из определений энергии (3) и cкалярного произведения (13):
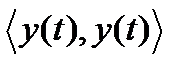 =
= 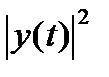 =
= 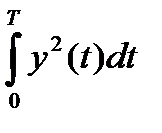 = Ey (1.14)
= Ey (1.14)
Векторы y(t) и x(t) ортогональны, если их скалярное произведение равно нулю:
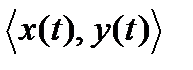 =
= 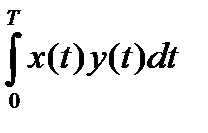 = 0 (1.15)
= 0 (1.15)
Базисные функции фi(t) изображаются в пространстве H векторами, которые формируют гиперплоскость Sn размерностью n, то есть набор функций фi (t) является неортогональным базисом гиперплоскости Sn. Разложение S из (1) всегда лежит в гиперплоскости Sn а коэффициенты Ci являются координатами S в неортогональном базисе гиперплоскости Sn. Разлагаемая функция f(t), в общем случае, не лежит в гиперплоскости Sn. Ошибка разложения d(t) изображается в пространстве H вектором, соединяющим концы векторов f(t) и S(t). Квадрат длины вектора ошибки, согласно (14), равен энергии ошибки, т.е. принятому критерию близости (4). Из геометрических соображений ясно, что длина 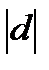 вектора ошибки (а вместе с ней и энергия ошибки) будет минимальной, если вектор ошибки d(t) ортогонален гиперплоскости Sn. Последнее выполняется, когда вектор ошибки d(t) ортогонален ко всем базисным функциям фi(t), формирующим гиперплоскость Sn. Принимая во внимание определение скалярного произведения (13) и условие ортогональности (15), можно записать:
вектора ошибки (а вместе с ней и энергия ошибки) будет минимальной, если вектор ошибки d(t) ортогонален гиперплоскости Sn. Последнее выполняется, когда вектор ошибки d(t) ортогонален ко всем базисным функциям фi(t), формирующим гиперплоскость Sn. Принимая во внимание определение скалярного произведения (13) и условие ортогональности (15), можно записать:
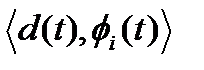 =
= 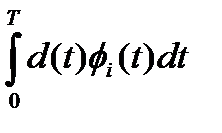 = 0
= 0
Легко видеть, что подставив сюда d(t) = f(t) – S(t) из (2) и используя обозначения (10), получим систему уравнений (9). Величины (10) при этом являются скалярными произведениями:
Ui,k = 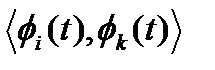 =
= 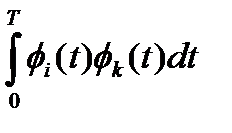 ; (1.16)
; (1.16)
Vi = 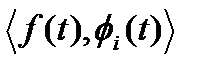 =
= 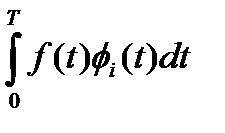 .
.
Матричная запись системы уравнений (9) имеет вид:
U*C = V (1.17)
Здесь U – квадратная матрица размерностью n*n с элементами Ui,k , V – вектор правых частей размерностью n*1 с элементами Vi , C– вектор неизвестных размерностью n*1 с элементами Ck..
Дата добавления: 2021-10-28; просмотров: 885;











