А. Первичная обработка исходной статистики
В соответствии с физическим определением плотности вероятности F(t) ее опытное значение F* в любой точке T = t1 рассчитывается по формуле
F(t=t1) 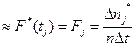 11
11
где 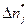 — число отказов, приходящихся на j-й интервал длиною
— число отказов, приходящихся на j-й интервал длиною 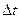 на оси возможных значений случайной величины Т (интервал
на оси возможных значений случайной величины Т (интервал 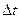 накрывает точку tj). Обычно точка tj выбирается в середине
накрывает точку tj). Обычно точка tj выбирается в середине 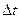 .
.
На этапе первичной обработки исходной статистики, исходя из формулы (11), необходимо определить:
— минимальное (tmin) и максимальное (tmax) значения из статистического ряда полученных величин Т=ti;
— длину частных интервалов группирования 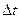 , на которые следует разбить весь полученный интервал R=tmax—tmin;
, на которые следует разбить весь полученный интервал R=tmax—tmin;
— значения величин 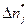 в каждом частном интервале
в каждом частном интервале 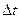 ;
;
— статистические значения элементов вероятности отказов для каждого интервала 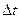 :
:
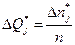 12
12
— опытные статистические значения F*;
— заполнить таблицу результатов первичной обработки статистики.
Значения tmin, tmax берутся непосредственно из полученного статистического ряда величин ti Длина всего интервала R = tmax- tmin дает первое представление о том, что наиболее вероятное значение случайной величины Т может быть заключено между tmin, tmax, т. е. неизвестная плотность вероятности F(t) распределена примерно в этом отрезке значений случайной величины Т.
Длина интервала At может быть ориентировочно выбрана с использованием эмпирической формулы:
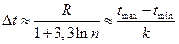 , 13
, 13
где k — число частных интервалов 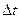 .
.
Значение числа k сначала ориентировочно оценивается по формуле k 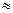 1 +3,3 lg n и обычно выбирается в пределах k =10
1 +3,3 lg n и обычно выбирается в пределах k =10 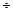 30.
30.
Подсчет количества реализаций 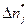 по интервалам группирования
по интервалам группирования 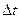 практически осуществляется следующим образом. Заблаговременно заготовляется бланк, образец которого дан в табл.10. Таблица разбивается на k колонок, представляющих собой интервалы
практически осуществляется следующим образом. Заблаговременно заготовляется бланк, образец которого дан в табл.10. Таблица разбивается на k колонок, представляющих собой интервалы 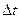 . Пусть, например, tmax=200 ч, tmin = 1 ч, тогда значения
. Пусть, например, tmax=200 ч, tmin = 1 ч, тогда значения 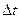 и k целесообразно выбрать следующие:
и k целесообразно выбрать следующие:
Δt ≈ (200 -1) /( 1+3,3 lg 100) ≈ 26 ч (принимаем Δt =20 ч)
K ≈ 1+ 3,3 lg 100 ≈ ( tmax – tmin )/ Δt ≈ (200-1)/20 ≈ 10.
Таблица 10 Экспериментальные данные примера
| ΔП*1 | ΔП*2 | ΔП*3 | … | … | … | ΔПj | … | … | ΔП | |||
| Количество статистических реализаций случайной величины t по интервалам Δt | X Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx | Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx Xx xx | X XX XX XX XX XX XX XX | X XX XX XX XX XX XX XX | X XX XX XX | X XX XX | XX XX | XX | XX | X | 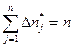
| |
| Значение середины интервалов Δt | tj | 210 230 | ||||||||||
| Величина интервалов | Δt | Δt’=60 | ||||||||||
| Статистическое значение вероятности отказов | ΔQ*j | ΔQ*1 | ΔQ*2 | ΔQ*3 | … | … | … | ΔQ*j | … | … | ΔQ*j | 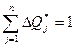
|
| Опытные значения плотности вероятности | F*j | F*1 | F*2 | F*3 | … | … | … | F*i | … | … | F*n | 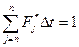
|
В каждой колонке приводится значение середины интервала
t1= tj (tj = 10; 30; 50; 70;90; 110; 130; 150; 170; 190) либо крайние правые границы интервалов tj+ 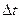 /2— (20; 40; 60; 80; 100;120; 140; 160; 180; 200). После этого рассматривается первое число из имеющегося неупорядоченного статистического ряда T=ti и определяется, к какому интервалу следует отнести это число. Например, t1 = 75 ч. В этом случае в четвертой колонке табл.10 с серединой tj = 70 ч и правой границей 80 ч ставится «крестик», а число ti = 75 ч вычеркивается из ряда. Затем рассматривается второе число ряда T = t2 и заносится «крестик» в соответствующую колонку табл.10 и т. д.
/2— (20; 40; 60; 80; 100;120; 140; 160; 180; 200). После этого рассматривается первое число из имеющегося неупорядоченного статистического ряда T=ti и определяется, к какому интервалу следует отнести это число. Например, t1 = 75 ч. В этом случае в четвертой колонке табл.10 с серединой tj = 70 ч и правой границей 80 ч ставится «крестик», а число ti = 75 ч вычеркивается из ряда. Затем рассматривается второе число ряда T = t2 и заносится «крестик» в соответствующую колонку табл.10 и т. д.
После того, как все n = 100чисел T=ti рассортированы по колонкам таблицы, производится подсчет чисел 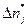 для каждого интервала
для каждого интервала 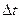 .
.
Пусть значения опытных чисел 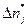 получены такие, как в табл. 10 (
получены такие, как в табл. 10 ( 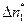 =31,
=31, 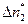 = 22,
= 22, 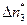 =13,
=13, 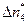 =13, затем 7, 5, 4, 2, 2 и 1). Разумеется, должно выполняться условие:
=13, затем 7, 5, 4, 2, 2 и 1). Разумеется, должно выполняться условие:

После того, как определены величины 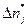 , необходимо проверить, нет ли слишком малых значений
, необходимо проверить, нет ли слишком малых значений 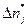 (например,
(например, 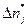 < 3
< 3 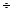 4). Так как малые значения дают недостаточную информацию об истинной закономерности распределения изучаемой случайной величины на этом интервале, то рекомендуется соседние интервалы с малым значением
4). Так как малые значения дают недостаточную информацию об истинной закономерности распределения изучаемой случайной величины на этом интервале, то рекомендуется соседние интервалы с малым значением 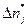 укрупнить в один, длина которого будет больше чем
укрупнить в один, длина которого будет больше чем 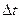 .
.
В нашем примере целесообразно последние три интервала объединить в один, длиной 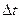 ' = 3
' = 3 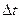 = 60 ч с новым числом
= 60 ч с новым числом 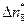 — 5. Окончательно имеем всего k = 8 интервалов, семь первых длиной по 20 ч и один последний длиной 60 ч.
— 5. Окончательно имеем всего k = 8 интервалов, семь первых длиной по 20 ч и один последний длиной 60 ч.
Теперь рассчитываются опытные значения элементов вероятности 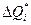 и
и 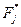 для всех интервалов, и результаты первичной обработки статистики заносятся в табл.10.
для всех интервалов, и результаты первичной обработки статистики заносятся в табл.10.
Б. Графическое изображение статистических данных
По результатам первичной обработки исходной статистики (табл.10) строится гистограмма, являющаяся наглядным представлением полученных исходных статистических данных. Гистограмма представляет собой графическую зависимость статистических значений 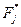 в точках T = tj. Значение функции
в точках T = tj. Значение функции 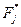 , принимается постоянным для всего интервала
, принимается постоянным для всего интервала 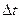 , поэтому графически гистограмма имеет вид отдельных прямоугольников с основанием шириной
, поэтому графически гистограмма имеет вид отдельных прямоугольников с основанием шириной 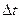 и высотой, равной
и высотой, равной 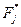 .
.
Гистограмма обладает рядом важных свойств:
— напоминает неизвестную искомую функцию F(t) т. е. 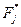
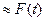 ,
,
— площадь, ограниченная гистограммой, равна единице, т. е.
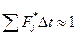 , 14
, 14
— используя гистограмму, можно определить среднестатистическое значение 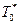 , которое примерно равно неизвестному значению средней наработки на отказ То (т. е. математическому ожиданию случайной величины T), по формуле:
, которое примерно равно неизвестному значению средней наработки на отказ То (т. е. математическому ожиданию случайной величины T), по формуле:
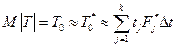 . 15
. 15
Гистограмма для рассмотренного примера изображена на рис. 16.
Так как опытное значение элемента вероятности отказа системы 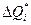 на интервале
на интервале 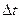 равно
равно 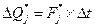 , то площадь любого прямоугольника гистограммы численно равна соответствующей величине
, то площадь любого прямоугольника гистограммы численно равна соответствующей величине 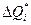
Величины 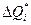 являются приближенной статистической оценкой неизвестных вероятностей отказов
являются приближенной статистической оценкой неизвестных вероятностей отказов 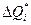 соответствующих элементов. Таким образом, построив гистограмму
соответствующих элементов. Таким образом, построив гистограмму 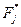 , получим первое наглядное представление о форме неизвестной функции F(t), т. е. гистограмма помогает сделать вывод об аналитической зависимости неизвестного закона F(t). Но пока еще неизвестен вид этого закона, т. е. его аналитическая форма.
, получим первое наглядное представление о форме неизвестной функции F(t), т. е. гистограмма помогает сделать вывод об аналитической зависимости неизвестного закона F(t). Но пока еще неизвестен вид этого закона, т. е. его аналитическая форма.
Дата добавления: 2021-07-22; просмотров: 732;











