Табличный контроллер
Если универсумы являются дискретными, то всегда имеется возможность вычислить значения управляющего сигнала для всех мыслимых комбинаций входных сигналов, перед тем как включить контроллер в работу. В контроллере, построенном с помощью таблицы, связи между всевозможными комбинациями входов и соответствующими выходами отображаются с помощью таблицы. При двух входных сигналах и одном выходе такая таблица является таблицей значений функции двух переменных. При трех входах таблица становится трехмерным массивом значений функции трех переменных. Табличная реализация нечеткого контроллера уменьшает время, требуемое для вычисления управляющего сигнала благодаря использованию таблицы, по крайней мере, тогда, когда на поиск требуемого значения управляющего сигнала в таблице не надо затрачивать много времени.
Ниже приведен пример таблицы функции двух переменных, соответствующий базовым правилам (2.2) совместно с функциями принадлежности терм-множеств, изображенных на рис. 2.8. Надо отметить, что в ячейках таблицы, которую можно назвать таблицей управления, размещены округленные до целых чисел значения управляющего сигнала, соответствующие значениям ошибки и скорости изменения ошибки, на пересечении которых находится ячейка. Так, если ошибка равна нулю и скорость изменения ошибки равна -50, то значение управляющего сигнала равно -61, что, разумеется, совпадает с округленным значением, полученным ранее с помощью механизма инференции (рис. 2.8). Почему разумеется?
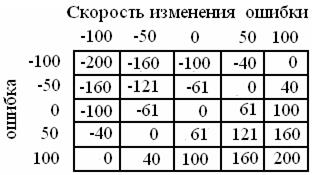
Потому что сама таблица заполнена за счет использования алгоритма нечеткого логического вывода.
Типичная область приложения табличных контролеров – та область, в которой в качестве входов фигурируют ошибка и скорость изменения ошибки. Табличный контроллер может быть встроен в крупный объект управления, например автомобиль, за счет использования технологии построения таблиц нескольких переменных.
Области таблицы. Касательно таблицы управления заметим, что отрицательные значения ошибки означают, что управляемая величина yпревышает заданное значение 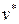 =const, так как ошибка e определяется соотношением e =
=const, так как ошибка e определяется соотношением e = 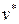 - y. Положительное значение ошибки говорит о том, что управляемая величина меньше заданного значения. Отрицательные значения скорости изменения ошибки означают, что управляемая величина увеличивается, а положительные значения − что уменьшается.
- y. Положительное значение ошибки говорит о том, что управляемая величина меньше заданного значения. Отрицательные значения скорости изменения ошибки означают, что управляемая величина увеличивается, а положительные значения − что уменьшается.

Некоторые области таблицы представляют особый интерес. Центр таблицы соответствует случаю, когда ошибка равна нулю, т.е. управляемая величина равна заданному значению. Кроме того, здесь скорость изменения ошибки тоже равна нулю, так что переходной процесс завершился и система пребывает в желаемом состоянии. Это устойчивое состояние равновесия. Диагональ, противоположная главной диагонали, является нулевой. Ей соответствуют желаемые состояния системы, когда имеет место устойчивое состояние равновесия, при котором управляемая величина равна заданному значению либо когда управляемая величина стремится (приближается) к заданному значению за счет инерционности объекта. Если управляемая величина немного отклонилась от значений, соответствующих нулевой диагонали, из-за помехи или возмущений, то контроллер будет создавать небольшие управляющие сигналы с целью вернуть систему в прежнее состояние. Если управляемая величина значительно отклонилась от заданного значения, и наблюдается тенденция к дальнейшему увеличению такого отклонения, то этим состояниям системы соответствуют верхний левый и правый нижний углы таблицы. В этих случаях, как видим, контроллер вносит весьма существенные изменения в управляющий сигнал. Числовые значения по обе стороны от нулевой диагонали не обязательно должны быть антисимметричны. Они могут быть произвольными, однако, отражающими асимметричную стратегию управления. При переходной характеристике с перерегулированием изменение положения точек кривой с координатами (ошибка, скорость изменения ошибки) будет отслеживать траектория перемещения от одной ячейки таблицы к другой в виде спирали, закручивающейся по часовой стрелке от левого нижнего угла таблицы по направлению к центру. Эта траектория подобна фазовой траектории на фазовой плоскости, по осям которой отложены ошибка и скорость изменения ошибки. Умелый проектировщик в течение настройки может так подобрать числовые значения управляющего сигнала, другими словами, так заполнить ячейки таблицы управления вручную, чтобы получить желаемое качество переходного процесса.
Билинейная интерполяция. Если квантование по уровню входов, осуществляемое с целью использования табличного контроллера, является грубым, т.е. с большим шагом квантования, то в системе будут иметь место предельные циклы, другими словами, незатухающие колебания в окрестности требуемого состояния равновесия. При этом таблица позволяет ошибке изменяться произвольно вблизи нулевого значения до тех пор, пока эти изменения не приведут к скачкообразному изменению нулевого значения управляющего сигнала на значение, соответствующее ячейке таблицы, соседней с центральной ячейкой. Этих неприятностей можно избежать, применяя билинейную интерполяцию между значениями таблицы управления, вместо того чтобы округлять входы до ближайшего целого значения, определяемого шагом квантования по уровню. В случае двухмерной таблицы управления пусть ошибка  e удовлетворяет условию
e удовлетворяет условию 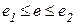 , где
, где 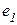 и
и 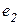 соседние значения ошибки, разделенные шагом квантования по уровню. Скорость изменения ошибки
соседние значения ошибки, разделенные шагом квантования по уровню. Скорость изменения ошибки 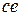 пусть аналогично удовлетворяет условию
пусть аналогично удовлетворяет условию 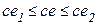 . Результирующее табличное значение управляющего сигнала тогда определяется с помощью линейной интерполяции по оси e между первой парой
. Результирующее табличное значение управляющего сигнала тогда определяется с помощью линейной интерполяции по оси e между первой парой 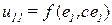 ,
, 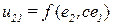 :
:
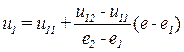
и второй парой значений 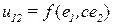 ,
, 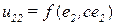 :
:
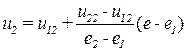 ,
,
и затем интерполяции по оси ce между парой значений u1, u2:
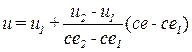 .
.
Дата добавления: 2021-01-11; просмотров: 589;











