Нечеткий контроллер с двумя входами и одним выходом
Рассмотрим нечеткий логический вывод для контроллера с двумя входами и одним выходом.
а) Нечеткий контроллер описывается одним правилом.
Пусть нечеткое правило является условным составным предложением следующего вида:
Если ошибка e есть 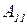 и скорость изменения ошибки ce есть
и скорость изменения ошибки ce есть 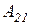 ,
,
То управление u есть 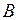 . (2.22а)
. (2.22а)
Как видим, нечеткий контроллер имеет два входа – ошибку и скорость ее изменения.
Правило (2.22а) можно записать в виде
Если вход e есть 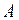 , то управление u есть
, то управление u есть 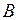 ,
,
где 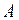 представляет собой конъюнкцию нечетких множеств
представляет собой конъюнкцию нечетких множеств 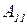 и
и 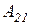 :
:
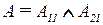 , (2.23)
, (2.23)
e –фиктивный вход, эквивалентый в некотором смысле двум входам.
Предположим, что в результате измерений установлено, что ошибка есть нечеткое множество 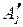 и скорость изменения ошибки есть нечеткое множество
и скорость изменения ошибки есть нечеткое множество 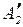 . Тогда можно считать, что нечеткому множеству
. Тогда можно считать, что нечеткому множеству 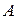 соответствует множество
соответствует множество
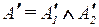 . (2.24)
. (2.24)
Степень истинности «утверждения 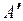 близко к A », другими словами, степень выполнения условия правила, определяется как конъюнкция степеней
близко к A », другими словами, степень выполнения условия правила, определяется как конъюнкция степеней 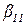 и
и 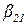 близости соответственно
близости соответственно 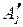 к
к 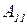 и
и 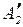 к
к 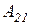 :
:
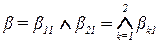 , (2.25)
, (2.25)
где
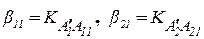 . (2.26)
. (2.26)
Операция (2.25) называется конъюнкцией условий или агрегированием условий.
Если 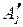 и
и 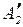 четкие множества (e и ce –четкие (количественные переменные) e’ и ce’), другими словами, синглтоны с ФП соответственно
четкие множества (e и ce –четкие (количественные переменные) e’ и ce’), другими словами, синглтоны с ФП соответственно
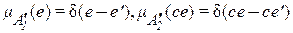 , (2.27)
, (2.27)
то степени истинности равны
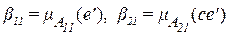 , (2.28)
, (2.28)
т.е. равны степеням принадлежности множеств 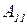 и
и 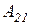 , полученным в процессе фаззификации.
, полученным в процессе фаззификации.
Нечеткий логический вывод определяется, как и прежде по (2.17),
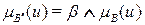 ,
,
где 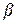 вычисляется с помощью (2.25). Если
вычисляется с помощью (2.25). Если 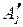 и
и 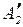 четкие множества, то
четкие множества, то
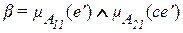 .
.
Лекция 10
б) Нечеткий контроллер описывается N правилами.
Если используется набор (множество) из N нечетких правил типа Если-То,
Если ошибка e есть 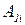 и скорость изменения ошибки ce есть
и скорость изменения ошибки ce есть 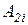 ,
,
То управление u есть 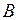 i ,
i , 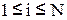 , (2.28a)
, (2.28a)
то находим нечеткие выводы по каждому правилу и затем образуем результат, т. е. нечеткий вывод по всему множеству правил как логическую сумму выводов (заключений), полученных по каждому правилу
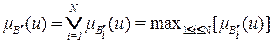 , (2.29)
, (2.29)
где
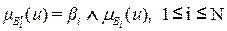 , (2.29,а)
, (2.29,а)
является нечетким выводом по i-му правилу. Сама операция (2.29) называется агрегированием выводов или аккумуляцией выводов.
В свою очередь значение
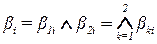 ,
, 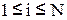 , (2.29,б)
, (2.29,б)
представляет собой степень истинности утверждения «нечеткое множество 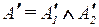 близко к множеству
близко к множеству 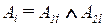 » или, другими словами, степень выполнения предпосылки i-го правила. Весь алгоритм максиминной инференции графически иллюстрируется для N=2 на рис. 2.7,б.
» или, другими словами, степень выполнения предпосылки i-го правила. Весь алгоритм максиминной инференции графически иллюстрируется для N=2 на рис. 2.7,б.
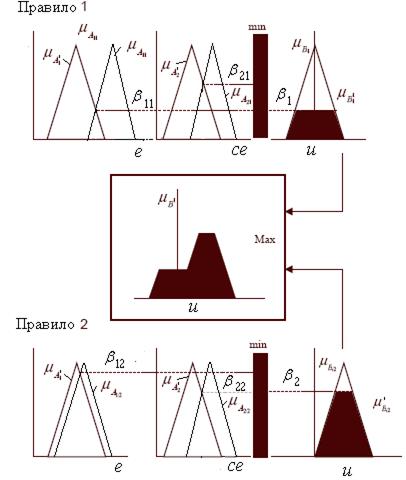
Рис. 2.7,б
Если e и ce – четкие (количественные переменные) соответственно e’ и ce’, так что имеет место (2.27), то
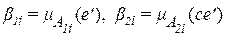 ,
, 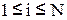 ,
,
так что
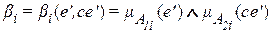 ,
, 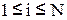 . (2.29,в)
. (2.29,в)
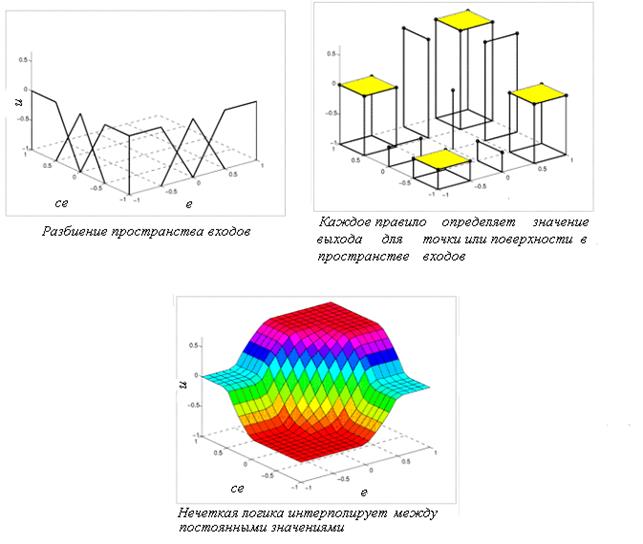
Разбиение пространства входов. Набор правил в форме конъюнкции условий (предпосылок), т. е. в форме 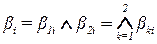 ,
, 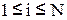 . (2.29,б) или
. (2.29,б) или 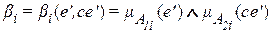 ,
, 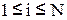 . (2.29,в), разделяет (разбивает) пространство входов (пространство условий) на решетку из областей (боксов), параллельных осям e и ce . Такое разбиение называется решетчатым разбиением. Каждый бокс является пересечением соответствующих терм.
. (2.29,в), разделяет (разбивает) пространство входов (пространство условий) на решетку из областей (боксов), параллельных осям e и ce . Такое разбиение называется решетчатым разбиением. Каждый бокс является пересечением соответствующих терм.

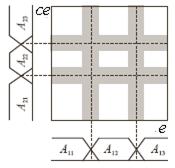
Рис. 2.7,в
Это показано на рис. 2.7,в в случае трех терм-множеств для каждой из переменных e и ce, имеющих трапециидальные функции принадлежности, причем используются N=9 правил. Кажется, можно ограничиться лишь тремя правилами. Однако тогда только три бокса, расположенные по диагонали, не смогут охватить все пространство входов (плоскость e,ce). Для того, чтобы накрыть все пространство входов, необходимо добавить еще 6 правил, комбинируя между собой все термы переменных e и ce.
На рис. 2.7,в слева функции принадлежностей терм не пересекаются, и каждый бокс соответствует своему правилу, другими словами, своему значению 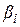 . Светлые участки на боксах определяются значениями
. Светлые участки на боксах определяются значениями 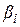 =1, а серые – значениями
=1, а серые – значениями 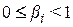 . На рис. 2.7,в справа функции принадлежности терм пересекаются (перекрываются) и здесь серые участки как раз определяются этими пересечениями. Отсюда серые участки принадлежат одновременно двум и более правилам, следовательно, отражают для таких правил значения
. На рис. 2.7,в справа функции принадлежности терм пересекаются (перекрываются) и здесь серые участки как раз определяются этими пересечениями. Отсюда серые участки принадлежат одновременно двум и более правилам, следовательно, отражают для таких правил значения 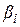 меньшие единицы.
меньшие единицы.
Если термами множества 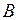 являются q (обычно q<N, т.е. число термов выхода меньше числа правил) синглтонов с ФП
являются q (обычно q<N, т.е. число термов выхода меньше числа правил) синглтонов с ФП
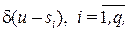 (2.30)
(2.30)
то нечеткий вывод (заключение) по всему множеству из N правил, иначе ФП множества 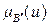 , определяется выражением
, определяется выражением
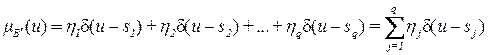 , (2.31)
, (2.31)
где величина
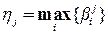 (2.32)
(2.32)
определяет возбуждающую силу j-го синглтона. Здесь 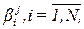 представляет собой элемент подмножества всех степеней истинности из множества степеней истинности
представляет собой элемент подмножества всех степеней истинности из множества степеней истинности 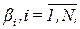 правил, которые соответствуют j-му синглтону (терму выхода со значением
правил, которые соответствуют j-му синглтону (терму выхода со значением 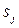 ). Дело в том, что при q < N несколько правил содержат в части То один и тот же синглтон.
). Дело в том, что при q < N несколько правил содержат в части То один и тот же синглтон.
Дата добавления: 2021-01-11; просмотров: 700;











