Многомерный нечеткий контроллер

В случае если контроллер имеет один выход u и r входов x₁, x₂,…,x_r, т.е., если каждая часть «Если» всех N правил

Если x₁ есть A_1i и x₂ есть A_2i и … x_r есть A_ri , то u есть B_i, ,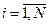

содержит r переменных, то ФП выхода для i- го правила определяется как

, ,

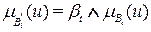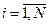где

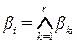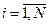, (2.32,а)

представляет собой конъюнкцию условий i-го правила, а композиция

, ,

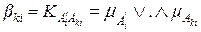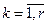показывает насколько близко множество 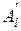к множеству 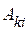. Здесь предполагается, что в результате измерений установлено, что x₁ есть нечеткое множество 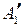, x₂ есть нечеткое множество 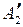, и, наконец, x_r есть нечеткое множество 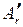, Принимая во внимание полученные выражения, приходим к формуле

,

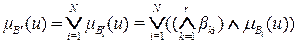позволяющей осуществить нечеткий логический вывод в самом общем случае. С учетом (2.32,а) последнюю формулу можно записать в более простом виде

.

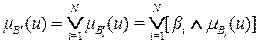Если все входы x_k , 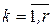, представляют собой четкие переменные 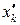, то

, .

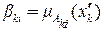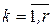Отсюда степень выполнения i-го правила

,

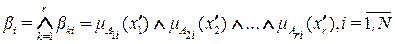и

.

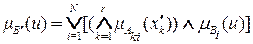Набор правил в форме конъюнкции условий (предпосылок), также как и в случае r=2, разбивает (разделяет) область входных сигналов на решетку, но теперь уже из нечетких «гипербоксов», параллельных осям x_k , 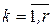. Каждый из «гипербоксов» представляет собой декартово произведение - пространство, образованное пересечением соответствующих одномерных нечетких множеств. Это показано на рис. 2.7,в для случая r=2 .

Кстати, число правил N, необходимых для обеспечения работоспособности нечеткого контроллера (охвата всей области входов), определяется по формуле

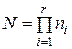, (2.32,б)

где r – количество входов, n_i – число термов для i-го входа.

Лекция №11

Визуализация алгоритма нечеткого логического вывода.Рассмотрим изложенную технологию инференции применительно к рис. 2.8 и 2.10.

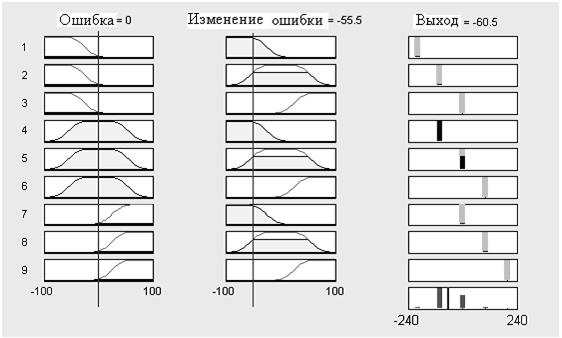
Рис. 2.8

Эти рисунки визуально отображают алгоритм, положенный в основу работы нечеткого ПД – контроллера. Например, первый ряд на рис. 2.8 говорит о том, что, если ошибка отрицательная (ряд 1, столбец 1) и скорость изменения ошибки отрицательная (ряд 1, столбец 2), то выход должен быть отрицательным и большим (по абсолютному значению).

Представленная на рис. 2.8 диаграмма целиком и полностью соответствует базовым правилам (2.2).

1.Если ошибка Отр и скорость изменения ошибки Отр, то выход ОтрБ.

2.Если ошибка Отр и скорость изменения ошибки Нуль, то выход ОтрС.

3.Если ошибка Отр и скорость изменения ошибки Пол, то выход Нуль.

4.Если ошибка Нуль и скорость изменения ошибки Отр, то выход ОтрС.(2.2)

5.Если ошибка Нуль и скорость изменения ошибки Нуль, то выход Нуль.

6.Если ошибка Нуль и скорость изменения ошибки Пол, то выход ПолС.

7.Если ошибка Пол и скорость изменения ошибки Отр, то выход ОтрБ.

8.Если ошибка Пол и скорость изменения ошибки Нуль, то выход ПолС.

9.Если ошибка Пол и скорость изменения ошибки Пол, то выход ПолБ.

В данном случае r=2 (ошибка и скорость изменения ошибки), число термов по каждому входу n₁ =n₂ =3, так что в соответствии с (2.32,б) требуемое число правил N=3*3=9. Число термов выхода q = 5.

Эти правила воплощают стратегию (закон) управления, согласно которому управляющий сигнал должен быть комбинацией упоминаемой ошибки и скорости изменения ошибки в нечетком пропорционально-дифференциальном контроллере.

Мгновенные значения ошибки и скорости ее изменения определяют положение вертикальных линий в первом и втором столбцах диаграммы. В рассматриваемом случае ошибка e= e’=0 и скорость ее изменения ce= =ce’ =-55.5. Для каждого правила алгоритм инференции отыскивает значения функций принадлежности в части условий (предпосылок, антецедент) правил, т.е. отыскивает степени принадлежности для каждого правила (синглтонная фаззификация).

Агрегирование (конъюнкция) условий. Агрегирование – операция, используемая для вычисления степени выполнения (истинности) или возбуждающей силы 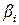условия i – го правила. Каждое правило, например правило 1, порождает степень принадлежности 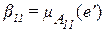, соответствующую измеренному значению ошибки, и степень принадлежности 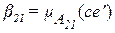, соответствующую измеренному значению скорости изменения ошибки. Тогда агрегирование согласно (2.25) и (2.28) является их конъюнкцией

.

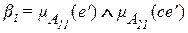Подобная операция осуществляется в отношении всех других правил. Агрегирование условий эквивалентно фаззификации, если контроллер имеет лишь один входной сигнал. Агрегирование условий иногда называют выполнением или вычислением возбуждающей силы левой части правил.

Активизация.Активизация (активация)-нечеткийлогический вывод (заключение) для каждого правила, возможно, связанный с ослаблением их возбуждающей силы. Длина черных вертикальных линий в третьем столбце на рис. 2.8 согласно формуле активизации (2.17) 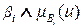определяет возбуждающую силу каждого i-го правила. Причем активизирована лишь часть синглтонов, а именно синглтоны, соответствующие первому, второму, четвертому, пятому, седьмому и восьмому правилам. В качестве операторов конъюнкции (активизации) используются операторы min или алгебраического произведения *, которым соответствует, как говорят, min-активизация и prod-активизация. В данном случае (рис. 2.8) вид используемого оператора не играет никакой роли, т.к. функциями принадлежности выхода (управляющего сигнала) являются

Рис.2.8

синглтоны.

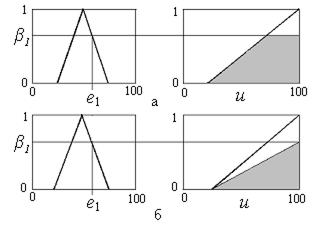
Рис. 2.9

Однако в общем случае в третьем столбце фигурируют функции принадлежности другого вида, например, 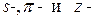образные функции принадлежности. При этом prod-активизация 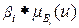(рис. 2.9,б) масштабирует график функции принадлежности выхода, таким образом, сохраняя его (графика) первоначальную форму и не ограничивая (не обрезая, не усекая) ее, как это имеет место при использовании min-активизации (рис. 2.9,а). Оба метода, в общем, работают хорошо, однако в результате использования операции алгебраического произведения (умножения) получаем несколько более сглаженный управляющий сигнал.

Правило с номером i может быть априорно взвешено с помощью весового коэффициента 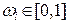, который называют степенью уверенности (доверия). При этом возбуждающая сила (степень истинности) такого правила изменяется и принимает вид,

.

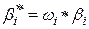Степень доверия определяется проектировщиком системы или обучающая программа пытается путем изменения этой степени адаптировать правила так, чтобы они в наибольшей мере соответствовали некоторой приемлемой зависимости вход-выход.

Аккумуляция.Аккумуляция, или аккумулирование представляет собой процедуру нахождения функции принадлежности выходной лингвистической переменной. Разумеется, что априорно выбираются функции принадлежности для всех 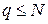, термов выходной переменной. Поэтому можно считать как бы априорно заданной лингвистическую переменную выхода контроллера. Цель аккумуляции состоит в том, чтобы объединить или аккумулировать заключения, лучше сказать подзаключения всех базовых правил, и в результате получить заключение, соответствующее всей правой части То этих правил. Подзаключения относятся к одной и той же лингвистической переменной выхода, но принадлежат различным правилам нечеткой инференции. После активизации функции принадлежности всех или части термов выхода видоизменяются в соответствии с входными сигналами контроллера. В сущности, каждое подзаключение полностью характеризуется видоизмененной функцией принадлежности соответствующего терма выхода. При этом надо иметь в виду, что каждому правилу отвечает свой терм выхода и свое подзаключение. Если правило не активизировано, то присущая ему видоизмененная функция принадлежности терма выхода равна нулю и не оказывает никакого влияния на искомое заключение. Еще стоит отметить, что одни и те же термы выхода с одинаковыми или различными видоизмененными функциями принадлежности могут фигурировать в нескольких правилах.

Для аккумуляции активизированных функций принадлежности терм выхода используется операция .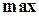

Замечание. Если видоизмененные функции принадлежности термов выхода не перекрываются между собой (например, в случае синглтонов), то операция аккумуляции применяется для определения функций принадлежности тех термов, которые встречаются в двух и более правилах инференции.

В результате аккумуляции получают заключения для всех термов переменной выхода. Теперь для определения искомой функции принадлежности выходной переменной достаточно расположить полученные функции принадлежности термов на одной оси. Таким способом найден окончательный график функции принадлежности управляющего сигнала (кстати, напомним, что в данном случае q=5, N=9), расположенный на рис. 2.8

Рис.2.8

внизу справа. Здесь один и тот же терм выхода ОтрС фигурирует во втором и четвертом правилах, терм выхода Нуль – в третьем, пятом и седьмом правилах, наконец, терм выхода ПолС – в шестом и восьмом правилах. Как видно из рис. 2.8, активизированы терм ОтрБ в первом правиле, второй терм ОтрС во втором и четвертом правилах, третий терм Нуль в пятом и седьмом правилах, четвертый терм ПолС в восьмом правиле. Все остальные термы во всех других правилах имеют нулевую функцию принадлежности.

Следовательно, применяя операцию max, получаем, что терму ПолБ соответствует подзаключение с нулевой функцией принадлежности; терму ОтрБ − подзаключение с функцией принадлежности, определяемой видоизмененной функцией принадлежности того же терма в первом правиле; терму ОтрС – подзаключение с функцией принадлежности, определяемой видоизмененной функцией принадлежности того же терма в четвертом правиле; терму Нуль – подзаключение с функцией принадлежности, равной видоизмененной функции принадлежности такого же терма в пятом правиле; терму ПолС - подзаключение с функцией принадлежности, определяемой функцией принадлежности того же терма в восьмом правиле. Искомую функцию принадлежности выхода согласно

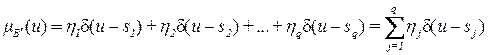(2.31)

и

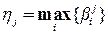(2.32)

можно записать так,

,

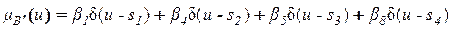в силу того, что

, , , .

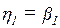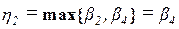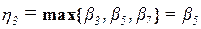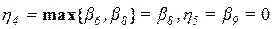Дефаззификация

Результирующее нечеткое множество выхода, определяемое функцией принадлежности, показанной на рис. 2.8 (внизу справа) и на рис. 2.10 (крайнее справа) должно быть преобразовано в четкое число (другими словами, качественная информация должна быть преобразована в количественную), которое может быть использовано как физическое значение управляющего сигнала. Такая операция называется дефаззификацией и на рис. 2.10 абсцисса точки, определяющей позицию белой разделительной линии, дает значение управляющего сигнала u = -35,9. Таким образом, результирующее нечеткое множество выхода «дефаззифицируется» в четкий управляющий сигнал.

Рис. 2.8

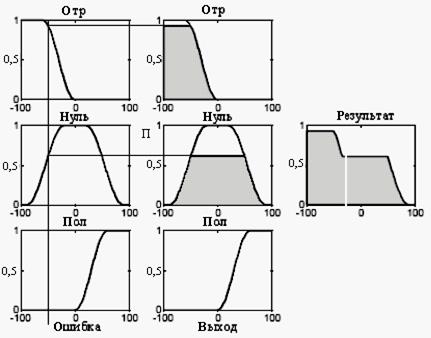
Рис. 2.10

Существуют несколько методов дефаззификации.

Центр тяжести (COG).В этом методе четкий выходной сигнал 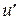(белая линия на рис. 2.10) есть абсцисса центра тяжести функции принадлежности результирующего нечеткого множества выхода

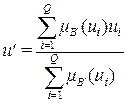, (2.33)

где 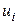− текущая точка в дискретном универсуме, 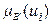− соответствующее значение степени принадлежности, Q – число элементов 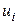в дискретном универсуме для управляющего сигнала. Выражение можно интерпретировать как взвешенное среднее значение элементов в опорном множестве. Разумеется, перед использованием формулы (2.33) надо осуществить дискретизацию

Для непрерывного случая суммирование заменяется интегрированием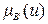

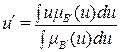. (2.34)

Здесь 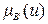− функция принадлежности нечеткого множества выхода после операции аккумуляции.

Этот метод является весьма полезным методом. Однако его вычислительная сложность, особенно применительно к (2.34), относительна велика. Его также называют центроид площади.

Лекция 12