Построение нечетких сумматоров

Для получения линейного преобразования вход-выход универсумы для входов должны быть шире диапазонов изменения входных сигналов, чтобы последние не выходили за пределы универсумов (не имело место явление насыщения). Кроме того, терм-множество каждого входа должно содержать некоторое число термов, проектируемых так, чтобы при любом значении входа сумма значений функций принадлежности всех термов была равна 1. Это условие соблюдается, если все термы, точнее их функции принадлежности, имеют треугольную форму и пересекаются с соседними функциями принадлежности при степени принадлежности =0,5. При этом пиковые (максимальные) значения (сердцевины) этих функций должны быть равноудалены друг от друга. Тогда каждому значению входа может соответствовать самое большее значения лишь двух функций принадлежности, и каждая из функций принадлежности между пиковыми значениями будет являться линейной функцией входного сигнала. Возьмем для примера следующие базовые правила.

1. Если e есть Пол и CE есть Пол, то выход u равен ,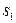

2. Если e есть Пол и CE есть Отр, то выход u равен 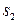, (2.38)

3. Если e есть Отр и CE есть Пол, то выход u равен ,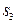

4. Если e есть Отр и CE есть Отр, то выход u равен .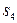

Здесь e − ошибка, ce − скорость изменения ошибки.

Предположим, что оба входных сигнала e и ce определены на стандартном универсуме [-100,100] и терм Пол имеет треугольную форму с пиковым значением 100 и абсциссой левой крайней точки основания (опоры) равной -100, а терм Отр имеет треугольную форму с пиковым значением -100 и абсциссой правой крайней точки основания равной 100 (рис. 2.14). В правилах (2.38) функции принадлежностей для терм Пол, соответствующих

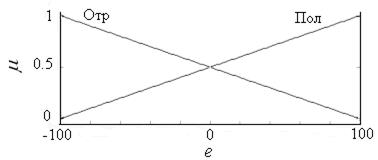
Рис. 2.14

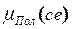четким входным сигналам e и ce, обозначим, как и . Операция агрегирования левой части первого правила вычисляет степень истинности

, (2.39)

где символ обозначает оператор нечеткого и.

Чтобы обеспечить линейность, для осуществления операций инужно применить алгебраическое произведение *. Число терм в каждом терм-множестве входов определяет число правил, т.к. они (правила) должны быть комбинацией операторов и(внутренним произведением) всех термов для обеспечения полноты (комплектности) правил. Множества (термы) выхода желательно выбирать в виде синглтонов, занимающих позиции 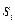, равные сумме позиций пиковых значений соответствующих входных терм.

1. Если e есть Пол и CE есть Пол, то выход u равен ,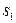

2. Если e есть Пол и CE есть Отр, то выход u равен 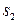, (2.38)

3. Если e есть Отр и CE есть Пол, то выход u равен ,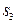

4. Если e есть Отр и CE есть Отр, то выход u равен .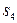

В данном примере для первого правила имеем два входных терма с функциями принадлежности и 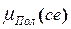, пиковые значения которых соответствуют значениям =100 и 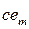=100. Следовательно, для первого правила 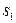= + + 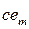=200. Аналогично для второго правила имеем две функции принадлежност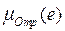и и 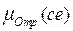. Для них пиковым значениям соответствуют позиции =100 и 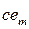= -100. Отсюда 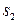=100 - 100=0. Таким же путем находим позиции остальных синглтонов: 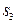= -100 +100 =0, 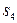= - 100 - 100 = -200. Итак, вектор позиций синглтонов для данного примера определяется выражением

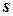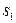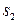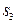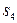= [ , , , ] = [200, 0, 0, -200]. (2.40)

Функции принадлежностей терм выхода могут в принципе иметь вид треугольников, симметричных относительно позиций, занимаемых их пиковыми значениями, однако для синглтонов проще осуществляется операция дефаззификации.

Аккумуляция (агрегирования выхода) в FIS Editor[2] системы MATLAB должна быть реализована с помощью операции sum, т.е. операции, связанной с вычислением граничной суммы (в пакете FuzTech[2] эта операция обозначается BSUM). Для первого правила из данного примера в результате операции sumполучаем min( 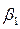,1) = .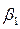

При использовании для дефаззификации метода центра тяжести (COG), кстати, в FIS Editor системы MATLAB этот метод обозначается как centroid, знаменатель в формуле, определяющей четкий (количественный) сигнал управления, не влияет на окончательный результат. Таким образом, сумма степеней истинности всех правил оказывается равной единице.

Все вышесказанное можно отнести к терм-множеству входов, включающих более двух терм. Дело в том, что при выполнении вышеприведенных условий в каждый момент времени будут активными лишь два терма.

Приведем доказательства аддитивности базовых правил для данного примера, полагая, что нечеткий логический вывод и функции принадлежности входов и выходов осуществляются в соответствии с вышерассмотренными требованиями. Возвращаясь к базовым правилам (2.38), определяем вклад первого правила в управляющий сигнал

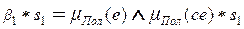= (2.41)

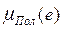
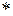
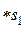= . (2.42)

Комбинация всех правил, иначе дефаззификация, осуществляемая с помощью метода центра тяжести COGS, приводит к

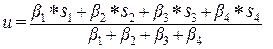. (2.43)

Чтобы упростить запись, введем обозначения

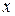= , (2.44)

= , (2.45)

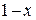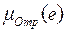= , (2.46)

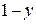= . (2.47)

В данном примере

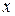= (e+100)/200, (2.48)

= (ce +100) /200. (2.49)

Если мы сложим агрегированные значения, определяемые первым и третьим правилами, входящие в знаменатель (2.43), то получим

= (2.50)

= . (2.51)

Найденный результат обусловлен специфическим выбором треугольных функций принадлежности. Аналогичным образом находим

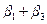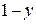= . (2.52)

Следовательно,

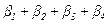=1 . (2.53)

Полученный результат объясняет, почему можно опустить знаменатель в (2.43), точнее положить его равным единице. Числитель (2.43) имеет вид

= (2.54)

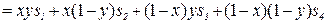. (2.55)

1. Если e есть Пол и CE есть Пол, то выход u равен ,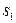

2. Если e есть Пол и CE есть Отр, то выход u равен 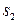, (2.38)

3. Если e есть Отр и CE есть Пол, то выход u равен ,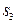

4. Если e есть Отр и CE есть Отр, то выход u равен .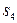

Очевидно, что 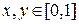, т.к. 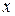и соответствуют правильным с точки зрения нечетких множеств функциям принадлежности. Поэтому функция (2.55) представляет собой линейную комбинацию четырех скалярных значений с коэффициентами, принадлежащими интервалу 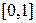. Так как 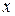является линейной функцией e, а линейной функцией ce, то числитель , следовательно, и выход u контроллера (управляющий сигнал) представляют собой линейную комбинацию e и ce, в данном примере сумму e и ce. Действительно, с учетом 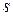= [ 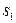, , 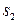, 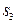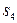] = [200, 0, 0, -200] (2.40) из (2.43) и (2.55) находим

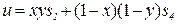
или

.

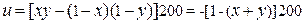Принимая во внимание

(2.48) 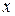= (e+100)/200 и (2.49) = (ce +100) /200 ,

получаем

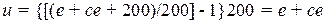. (2.56)

Как видим, рассмотренная методика конструирования нечеткого контроллера приводит, в сущности, к нечеткому сумматору, осуществляющему суммирование двух сигналов, в данном случае e и ce. Выражение (2.56) можно трактовать как выход линейного ПД - контроллера с равными единице коэффициентами усиления.

В общем случае можно разработать базовые правила, обеспечивающие линейное преобразование вход-выход. При этом такая методика конструирования нечеткого контроллера приводит, по сути, к нечеткому сумматору, осуществляющему суммирование двух сигналов, в данном случае e и ce. Следующий перечень пунктов резюмирует основные принципы проектирования, позволяющие сконструировать нечеткие правила, эквивалентные суммированию входных сигналов.

· Используйте для терм входов функции принадлежности треугольной формы, пересекающиеся при 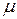= 0,5.

· Используйте алгебраическое произведение * для реализации операции и;

· Базовые правила должны быть полной комбинацией связок и (декартовым произведением) всех входных термов.

· Используйте в качестве термов выхода синглтоны, их позиции определяйте как сумму позиций пиковых значений функций принадлежности терм входа.

· Используйте для дефаззификации метод центра тяжести COGS.

2.6 Проектирование нечетких ПИД-контроллеров

Если цель управления заключается в стабилизации управляемой величины на заданном уровне, то естественно рассматривать ошибку управления в качестве входного сигнала для нечеткого контроллера, и отсюда вытекает мысль о том, что и производная и интеграл от ошибки управления также могут быть использованы как входные сигналы для такого контроллера. При этом мы приходим к идее построения нечеткого ПИД- контроллера.

Однако при настройке нечеткого ПИД-контроллера трудно судить о влиянии каждого из его параметров (коэффициентов усиления) на такие показатели качества, как перерегулирование, длительность переходного процесса, в силу того, что этот контроллер в большинстве случаев обладает ярко выраженными нелинейными свойствами, и, кроме того, имеет большое число настраиваемых параметров. В этом разделе предлагается процедура, позволяющая трансформировать технологию выбора параметров в области ПИД- регуляторов в область нечетких контроллеров. Основная идея заключается в том, чтобы, начав проектирование с настройки обычного (четкого) ПИД-регулятора, заменить его эквивалентным линейным нечетким контроллером, затем преобразовать линейный контроллер в нелинейный нечеткий контроллер, и, в конечном счете, настроить должным образом последний контроллер. Описанный здесь подход уместен, если четкий ПИД-регулятор в принципе может быть использован в целях управления данным объектом или уже применяется. Систематическая процедура настройки, сопровождающая такой подход, упрощает выбор параметров нечеткого контроллера и может служить мостом на пути автонастройки последнего.

Классические контроллеры могут быть настроены различными способами, включая ручную настройку, метод Циглера-Николса, формирование частотной характеристики разомкнутой системы, аналитические методы (путем оптимизации), метод размещения нулей и полюсов или с помощью автонастройки. Надо отметить, что при определенных условиях работы, свойства четких ПИД-регуляторов и нечетких ПИД-контроллеров оказываются весьма схожими. Тем не менее, следует признать существование большого разрыва между методами настройки ПИД-регуляторов и стратегией проектирования нечетких ПИД-контроллеров.

В этом разделе рассматривается технология проектирования, которая на первом этапе связана с использованием известной технологии проектирования ПИД-регуляторов.

Кажется разумным начать проектирование нечеткого контроллера с проектирования четкого ПИД-регулятора, может быть даже с П-регулятора, и добиться за счет выбора его параметров устойчивости замкнутой системы. От достигнутого результата легче перейти к нечеткому управлению. Каждый этап предлагаемого метода настройки нечеткого регулятора будет подробно рассмотрен в последующих параграфах.

Лекция 14