Интегрирование тригонометрических выражений

1. Интегралы вида ; ; ,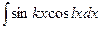

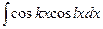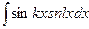где k, l – действительные числа.

Интегралы решаются с помощью применения тригонометрических формул:

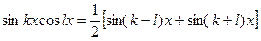
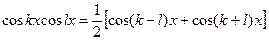
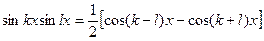
Примеры:

1)

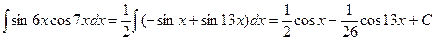
2)

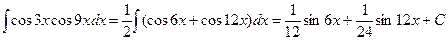
3)

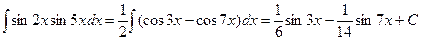
2. Интегралы вида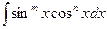

Рассмотрим 4 случая:

1) m – нечетное положительное число, т.е. 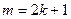. Подынтегральное выражение преобразовываем так:

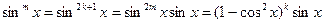
В интеграле переходим к новой переменной интегрирования: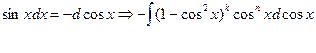

2) показатель степени косинуса n – нечетное положительное число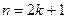

Тогда:

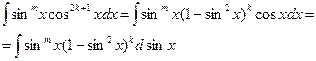
3) Сумма 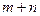показателей степеней синуса и косинуса четное отрицательное число .

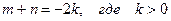В этом случае подынтегральная функция может иметь два вида:

- подынтегральная функция дробь, в числителе которой находится степень синуса, а в знаменателе – степень косинуса (или наоборот), причем показатели степени или оба четные или оба нечетные. В этом случае говорят, что они одинаковой четности. Так как 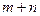- отрицательное число, то отсюда следует, что степень знаменателя больше степени числителя.

- подынтегральная функция дробь, числитель которой постоянная величина, а знаменатель – произведение степеней синуса и косинуса одинаковой четности.

В рассматриваемом случае ( 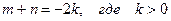) любая из подстановок 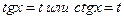преобразует подынтегральную функцию в многочлен или многочлен, сложенный с целыми отрицательными степенями некоторой независимой переменной t

Если подынтегральная функция имеет первый из разобранных видов, а в числителе находится степень sinx, более удобной из этих подстановок является tgx=t, если же в числителе находится степень cosx, рациональнее применить ctgx=t.

Дроби второго вида с помощью указанных подстановок можно привести к интегрированию степенных функций.

Если применять подстановку tgx=t, надо учесть:

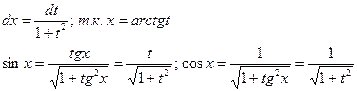
Если применяется подстановка ctgx=t, то

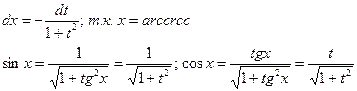
4) Сумма показателей степеней синуса и косинуса равны по абсолютной величине, но противоположны по знаку, а подынтегральное выражение имеет один из видов 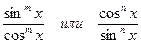. Если m>0, то интеграл приводится к виду 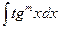, а если n>0 – к интегралу .

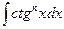В первом интеграле применяют подстановку tgx=t, .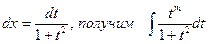

Во втором интеграле применяют подстановку сtgx=t, .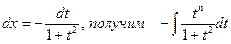

Примеры

1)

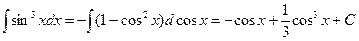
2)

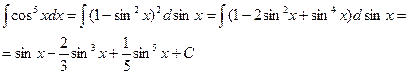
3)

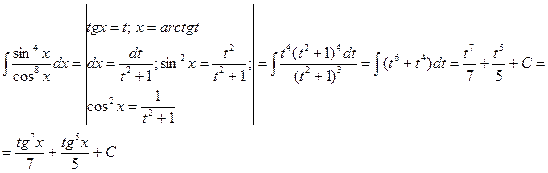
4)

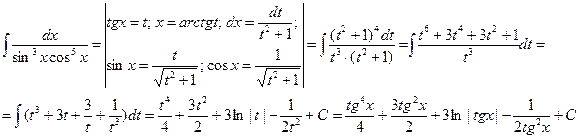
5)

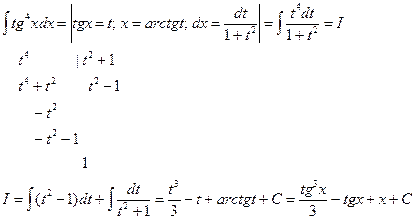
Лекция 8