Определенный интеграл как предел интегральной суммы
Пусть дана функция 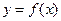 , определенная на отрезке [a;b], где a<b. Разобъем отрезок [a;b] на частичные отрезки произвольной длины [x0;x1], [x1;x2],…, [xn-1;xn], так что x0=a, xn=b (x0<x1<…<xn). На каждом частичном отрезке выбираем произвольную точку
, определенная на отрезке [a;b], где a<b. Разобъем отрезок [a;b] на частичные отрезки произвольной длины [x0;x1], [x1;x2],…, [xn-1;xn], так что x0=a, xn=b (x0<x1<…<xn). На каждом частичном отрезке выбираем произвольную точку 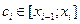 и вычислим значения функции в каждой из этих точек
и вычислим значения функции в каждой из этих точек 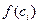 . Составим произведения
. Составим произведения 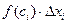 , где
, где 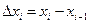 - длина частичного отрезка. Составим сумму всех таких произведений:
- длина частичного отрезка. Составим сумму всех таких произведений:
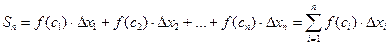
Эта сумма называется интегральной суммой функции 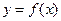 на отрезке [a;b].
на отрезке [a;b].
Обозначим частичный отрезок наибольшей длины 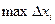 . Будем увеличивать число разбиений отрезка [a;b] на частичные отрезки, т.е. n→∞, не изменяя длину самого отрезка [a;b]. При этом
. Будем увеличивать число разбиений отрезка [a;b] на частичные отрезки, т.е. n→∞, не изменяя длину самого отрезка [a;b]. При этом 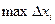 →0. Найдем при этих условиях
→0. Найдем при этих условиях 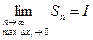 . Предел частичной суммы, если он существует, не зависит ни от способа разбиения отрезка [a;b] на частичные отрезки, ни от выбора точек на них. Этот предел называется определенным интегралом от функции
. Предел частичной суммы, если он существует, не зависит ни от способа разбиения отрезка [a;b] на частичные отрезки, ни от выбора точек на них. Этот предел называется определенным интегралом от функции 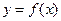 на отрезке [a;b] и обозначается:
на отрезке [a;b] и обозначается:
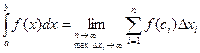
Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования, [a;b] – область интегрирования.
Теорема Коши. Если функция 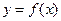 непрерывна на отрезке [a;b], то определенный интеграл
непрерывна на отрезке [a;b], то определенный интеграл 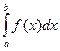 существует.
существует.
Непрерывность функции является достаточным условием ее интегрируемости. Однако, определенный интеграл может существовать и для некоторых разрывных функций, в частности, для всякой ограниченной на отрезке функции, имеющем на нем конечное число точек разрыва.
Из определения определенного интеграла следуют свойства:
- определенный интеграл не зависит от обозначения переменной интегрирования 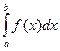 =
= 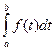 =
= 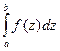 , так как интегральная сумма не зависит от того, какой буквой обозначить ее аргумент;
, так как интегральная сумма не зависит от того, какой буквой обозначить ее аргумент;
- определенный интеграл с одинаковыми пределами интегрирования равен нулю 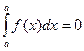 , так как длина отрезка равна нулю;
, так как длина отрезка равна нулю;
- для любого действительного числа с: 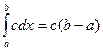 , так как при этом
, так как при этом 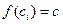 .
.
Дата добавления: 2021-01-11; просмотров: 610;











