Все знаки угловых и линейных кинематических параметров, полученных в результате решения аналитических выражений, относятся к выбранной системе координат.
Задачи кинематического исследования
Основным назначением механизмов является выполнение необходимых движений, которые описываются посредством его кинематических характеристик. К ним относятся траектории движения точек и звеньев механизма, координаты точек, перемещения точек и звеньев, их скорости и ускорения. К числу кинематических параметров относятся также и такие, которые не зависят от закона движения ведущего звена, а определяются только строением механизма, размерами его звеньев и, в общем случае, зависят от положения ведущего звена. Это аналоги скоростей и ускорений или передаточные функции.
По кинематическим характеристикам можно сделать вывод о том, насколько успешно выполнена одна из основных задач проектирования механизма – выбор структурной схемы и определения размеров звеньев.
Знание кинематических характеристик важно также для динамических расчетов.
Существует несколько методов определения кинематических характеристик:
1. Графические
2. Аналитические
3. Экспериментальные
1. Кинематическое исследование методом планов скоростей и ускорений.
Графические методы расчетов обладают наглядностью и отличаются удобством контроля. Иногда только графические методы дают наиболее простое решение. Точность графических методов 0,3…0,5% (при большом желании) достаточно для решения многих практических задач. Использование компьютерной графики позволяет повысить точность расчётов на порядок.
Следствие из принципа Ассура.
Если при кинематическом исследовании рассматривать вначале ведущее звено, затем первую присоединенную группу, затем по группам в порядке их присоединения, то в каждой группе будут известными кинематические параметры любой точки, принадлежащей свободным элементам кинематических пар группы.
Действительно, так как свободные элементы в кинематических парах группы присоединяются к ведущему звену и к стойке, кинематические параметры которых известны.
Т.е. каждая группа будет кинематически определимой цепью.
Лемма 1.
(Гречес. вспомогат.
предложение, помо-
гающ. при док-ве)
|
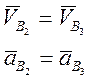
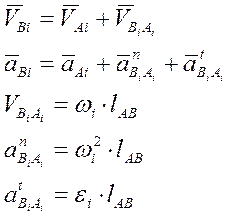
|
.
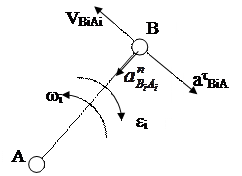
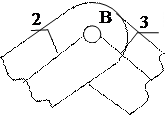
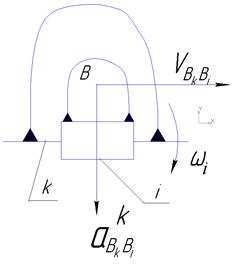 Лемма 3. Если два звена связаны поступательной кинематической парой, то угловые перемещения, скорости и ускорения этих звеньев равны между собой, а относительные скорости и ускорения двух точек, расположенных одна над другой имеют направления коллинеарное с направлением оси поступательной пары.
Лемма 3. Если два звена связаны поступательной кинематической парой, то угловые перемещения, скорости и ускорения этих звеньев равны между собой, а относительные скорости и ускорения двух точек, расположенных одна над другой имеют направления коллинеарное с направлением оси поступательной пары.
φi = φk ωi = ωk εi = εk
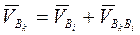
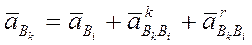

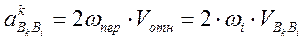
Для определения направления вектора Кариолисова ускорения нужно вектор относительной скорости повернуть на 900 по направлению угловой скорости переносного движения.
1.1. Построение планов скоростей и ускорений для механизмов с группой 1 вида, 2кл., 2 пор.
Планом скоростей (ускорений) называется система векторов скоростей (ускорений), характерных точек механизма, отложенных из одной точки (полюса), в данном его положении.
Построение планов скоростей и ускорений, руководствуясь следствием из принципа Ассура, начинаем с ведущего звена. При этом принимаем ω1 = const (угловая скорость ведущего звена) и, соответственно, ε1 = 0.
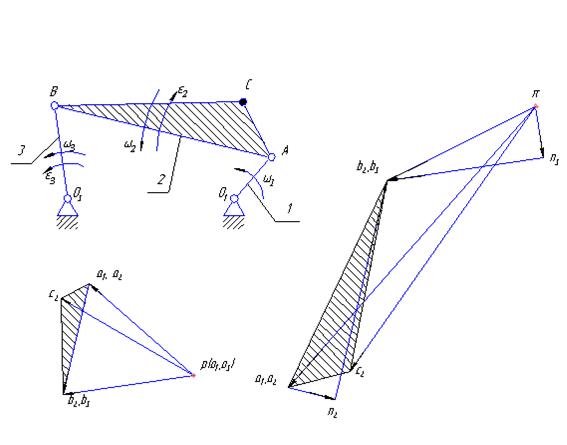
Полюс плана скоростей обозначается латинской буквой p, а плана ускорений греческой буквой π. Концы векторов на планах скоростей и ускорений обозначаются теми же буквами, что и точки, только строчными.
Скорость точки А, принадлежащей первому звену, определяется по выражению 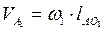 и направлена перпендикулярно АО1, в сторону вращения ведущего звена.
и направлена перпендикулярно АО1, в сторону вращения ведущего звена.
План скоростей первой присоединённой группы строится на основании леммы 1 и леммы 2.
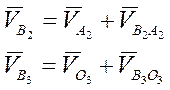 По лемме 1:
По лемме 1: 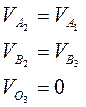 По лемме 2 :
По лемме 2 :
Ускорение точки А, принадлежащей первому звену, определяется по выражению 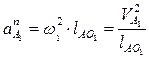 , так как ε1 = 0и, следовательно,
, так как ε1 = 0и, следовательно, 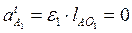 и направлено параллельно АО1, в сторону центра вращения ведущего звена.
и направлено параллельно АО1, в сторону центра вращения ведущего звена.
Векторные уравнения планов ускорений составляются в соответствии с векторными уравнениями планов скоростей.
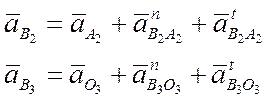
Планы положений механизма, планы скоростей и ускорений чертятся с определённым масштабным коэффициентом, а не рисуются. При выборе масштабных коэффициентов руководствуются теми же принципами, что и при выполнении любых чертежей – наилучшее использование поля чертежа.
При выполнении планов положений рекомендуется брать стандартный масштаб. При построении планом скоростей и ускорений масштабный коэффициент может быть любой, удобный для пользования.
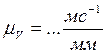 ,
, 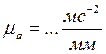
Из плана скоростей можно определить величину и направление угловых скоростей 2-го и 3-го звена.
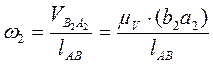
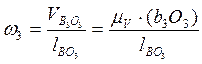
Где (b2a2) и (b3o3) – отрезки, измеряемые на плане скоростей в мм, а lAB и lBO3 – действительная длина звеньев.
Направление угловых скоростей можно определить, если вектора относительных скоростей, мысленно, перенести на план положения механизма в точку В.
Зная угловые скорости звеньев, можно определить нормальные ускорения точки В относительно А и О3.
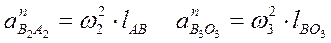
Нормальные ускорения обозначаются буквой ncиндексом того звена, по которому они направлены (см. рисунок). Тангенциальные (касательные) ускорения не обозначаются.
Из плана ускорений можно найти величину и направление угловых ускорений звеньев.
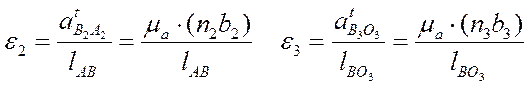
Направления угловых ускорений можно определить, если мысленно перенести тангенциальные ускорения на план положения механизма в точку В.
Скорость и ускорение точки Сможно построить, используя теорему о конгруэнтности.
Теорема: Если три точки расположены на одном звене, то концы векторов скоростей и ускорений тех же точек располагаются на вершинах конгруэнтных треугольников (обход вершин совпадает, а одноимённые углы равны).
1.2. Построение планов скоростей и ускорений для механизмов с группой 2 вида, 2кл., 2 пор.

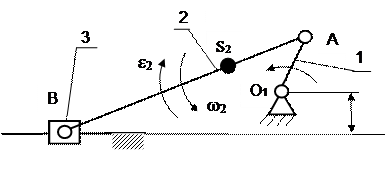
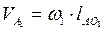
ω1 = const, ε1 = 0. 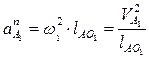
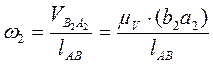

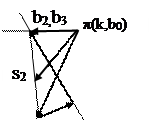 | |||
| |||
|
|
| |||
| |||
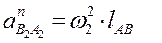
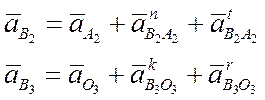
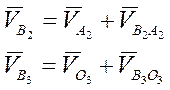
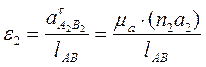
Скорость и ускорение центра масс второго звена (S2) можно определить из конгруэнтных треугольников AS2B и as2b
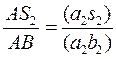
Где длина отрезка (ab) измеряется непосредственно на плане скоростей (ускорений).
Направление угловой скорости и углового ускорения шатуна (звено 2) определяется так же, как и в предыдущей группе.
1.3. Построение планов скоростей и ускорений для механизмов с группой 3 вида, 2кл., 2 пор.
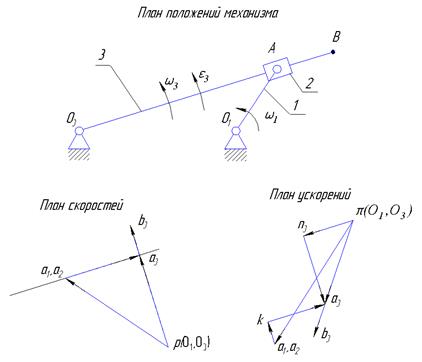
Векторные уравнения для построения планов скоростей и ускорений и формулы для определения промежуточных кинематических параметров
ω1 = const, ε1 = 0. 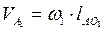
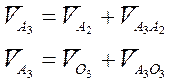
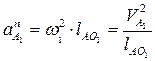
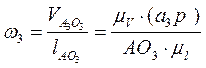
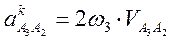
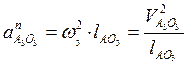
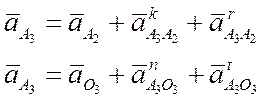
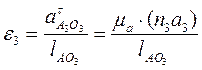
Скорость и ускорение точки В можно построить, используя теорему о конгруэнтности по которой
1.4. Построение планов скоростей и ускорений для механизмов с группой 4 вида, 2кл., 2 пор.
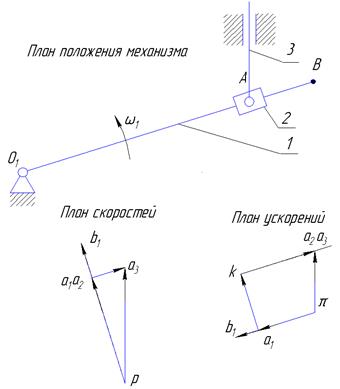
Векторные уравнения для построения планов скоростей и ускорений и формулы для определения промежуточных кинематических параметров
ω1 = const, ε1 = 0. 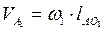
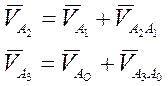
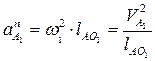
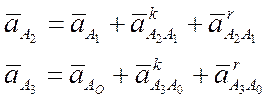
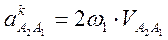
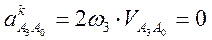 так как ω3 = 0
так как ω3 = 0
1.5. Построение планов скоростей и ускорений для механизмов с группой 5 вида, 2кл., 2 пор.
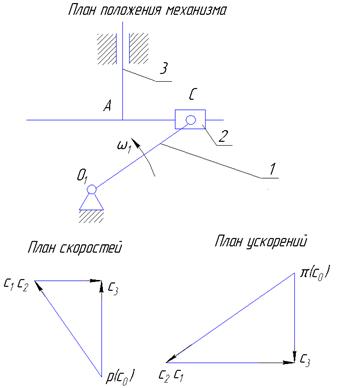
Векторные уравнения для построения планов скоростей и ускорений механизма с группой 5 вида и формулы для определения промежуточных кинематических параметров
ω1 = const, ε1 = 0. 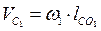
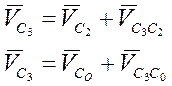
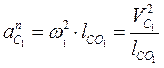
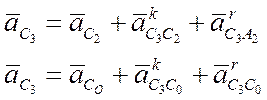
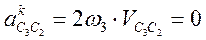 так как ω3 = 0
так как ω3 = 0
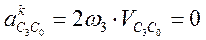 так как ω3 = 0
так как ω3 = 0
Обобщая вышеприведенные построения планов скоростей можно увидеть, что векторные уравнения для планов скоростей составляются для точек, скорости которых неизвестны и обязательно связанных с вращательными кинематическими парами. Векторные уравнения для планов ускорений составляются по векторным уравнениям для планов скоростей и, как правило, это больших трудностей не вызывает.
Порядок кинематического исследования механизмов методом планов скоростей и ускорений.
1. Построить кинематическую схему механизма для заданного положения ведущего звена (вычертить точно по размерам в каком то масштабе).
2. Провести структурный анализ механизма.
3. Для каждой группы составить векторные уравнения планов скоростей и планов ускорений.
4. Построить план скоростей ведущего звена.
5. По векторным уравнениям построить план скоростей первой присоединённой группы, затем второй и т.д. по группам в порядке их присоединения.
6. Построить план ускорений ведущего звена.
7. По векторным уравнениям построить план ускорений первой присоединённой группы, затем второй и т.д. по группам в порядке их присоединения.
8. Определить кинематические параметры, указанные в задаче.
Рассмотрим построение плана скоростей и ускорений на примере механизма поперечно-строгального станка.
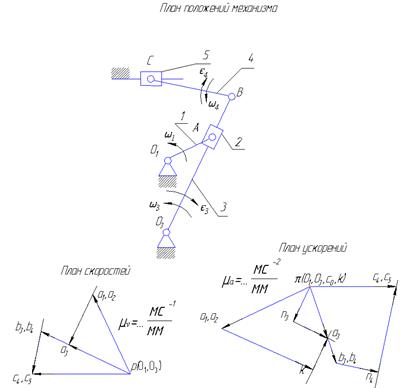
Строим план скоростей
Строим план скоростей для ведущего звена, для которого ω1 = const, ε1 = 0. 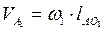 . Вектор скорости точки А направляем в сторону угловой скорости первого звена перпендикулярно отрезку АО1. Длина вектора (ра1) c учётом выбранного масштабного коэффициента μv
. Вектор скорости точки А направляем в сторону угловой скорости первого звена перпендикулярно отрезку АО1. Длина вектора (ра1) c учётом выбранного масштабного коэффициента μv 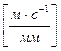 будет равна
будет равна
(ра1) = 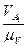 [мм]
[мм]
Строим план скоростей для первой присоединённой группы (группа 3 вида, 2 класса, 2 порядка).
Векторные уравнения для этой группы
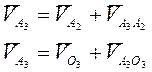
Решаем эту систему векторных уравнений. Скорость точки А2 = А1, т.е. уже отложена. Вектор относительной скорости 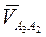 начинается в конце вектора А2, параллельна оси поступательной пары А, направление пока неизвестно. Скорость точки О3 известна (она равна нулю, т.е. вектор этой скорости начинается и заканчивается в полюсе плана). Вектор относительной скорости
начинается в конце вектора А2, параллельна оси поступательной пары А, направление пока неизвестно. Скорость точки О3 известна (она равна нулю, т.е. вектор этой скорости начинается и заканчивается в полюсе плана). Вектор относительной скорости 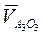 начинается в конце вектора
начинается в конце вектора 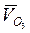 , т.е. в полюсе, перпендикулярен отрезку АО3 и заканчивается на пересечении с относительной скоростью
, т.е. в полюсе, перпендикулярен отрезку АО3 и заканчивается на пересечении с относительной скоростью 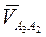 . Пересечение относительных скоростей
. Пересечение относительных скоростей 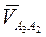 и
и 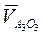 даёт конец вектора скорости
даёт конец вектора скорости 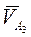 .
.
Скорость точки В3 определяем из пропорции (теорема о конгруэнтности)
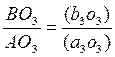
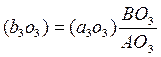
Здесь отрезок 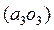 берём из плана скоростей, а отрезки ВО3 и АО3 из плана положений механизма.
берём из плана скоростей, а отрезки ВО3 и АО3 из плана положений механизма.
Если мысленно перенести вектор относительной скорости 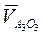 в точку А, то можно определить направление угловой скорости третьего звена, величина которой равна
в точку А, то можно определить направление угловой скорости третьего звена, величина которой равна
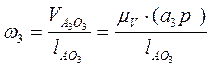
Строим план скоростей второй присоединённой группы (группа 2 вида, 2 класса, 2 порядка).
Векторные уравнения для этой группы
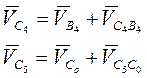
Скорость точки В4 известна и равна скорости точки В3. Вектор относительной скорости 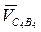 начинается в конце вектора
начинается в конце вектора 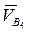 , перпендикулярен отрезку АВ, направление пока неизвестно. Скорость точки Со известна (она равна нулю, т.е. вектор этой скорости начинается и заканчивается в полюсе плана). Вектор относительной скорости
, перпендикулярен отрезку АВ, направление пока неизвестно. Скорость точки Со известна (она равна нулю, т.е. вектор этой скорости начинается и заканчивается в полюсе плана). Вектор относительной скорости 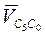 начинается в конце вектора
начинается в конце вектора 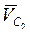 , т.е. в полюсе, и параллелен оси поступательной пары С. Пересечение относительных скоростей
, т.е. в полюсе, и параллелен оси поступательной пары С. Пересечение относительных скоростей 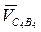 и
и 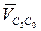 даёт конец вектора скорости
даёт конец вектора скорости 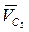 .
.
Если мысленно перенести вектор относительной скорости 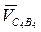 в точку С, то можно определить направление угловой скорости четвёртого звена, величина которой равна
в точку С, то можно определить направление угловой скорости четвёртого звена, величина которой равна
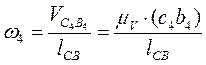
Строим план ускорений.
Строим план ускорений ведущего звена, для которого ω1 = const, ε1 = 0.Ускорение точки А, принадлежащей первому звену, определяется по выражению 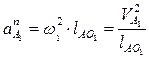 , так как ε1=0и, следовательно,
, так как ε1=0и, следовательно, 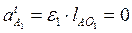 и направлено параллельно АО1, в сторону центра вращения ведущего звена. Длина вектора (πа1) c учётом выбранного масштабного коэффициента μа
и направлено параллельно АО1, в сторону центра вращения ведущего звена. Длина вектора (πа1) c учётом выбранного масштабного коэффициента μа 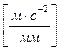 будет равна (πа1) =
будет равна (πа1) = 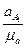 [мм]
[мм]
Строим план ускорений для первой присоединённой группы.
Векторные уравнения планов ускорений составляются в соответствии с векторными уравнениями планов скоростей.
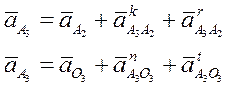
Решаем эту систему векторных уравнений. Ускорение точки А2 равно ускорению точки А1, т.е. уже отложено. Вектор ускорения Кориолиса 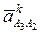 начинается в конце вектора А2 и определяется по выражению
начинается в конце вектора А2 и определяется по выражению 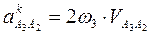 . Для определения направления этого ускорения необходимо взять (мысленно) вектор относительной скорости
. Для определения направления этого ускорения необходимо взять (мысленно) вектор относительной скорости 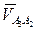 , совместить его с осью поступательной пары А и повернуть на 900 в сторону угловой скорости ω3. Вектор радиального ускорения
, совместить его с осью поступательной пары А и повернуть на 900 в сторону угловой скорости ω3. Вектор радиального ускорения 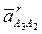 начинается в конце вектора Кориолиса, параллелен оси поступательной пары А, направление пока неизвестно. Ускорение точки О3 известно (оно равно нулю, т.е. вектор этого ускорения начинается и заканчивается в полюсе плана). Вектор нормального ускорения, равный
начинается в конце вектора Кориолиса, параллелен оси поступательной пары А, направление пока неизвестно. Ускорение точки О3 известно (оно равно нулю, т.е. вектор этого ускорения начинается и заканчивается в полюсе плана). Вектор нормального ускорения, равный 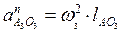 начинается в конце вектора
начинается в конце вектора 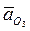 , т.е. в полюсе, параллелен отрезку АО3. Вектор тангенциального ускорения
, т.е. в полюсе, параллелен отрезку АО3. Вектор тангенциального ускорения 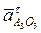 начинается в конце нормального
начинается в конце нормального 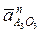 и заканчивается на пересечении с радиальным ускорением
и заканчивается на пересечении с радиальным ускорением 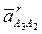 . Пересечение относительных ускорений
. Пересечение относительных ускорений 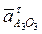 и
и 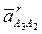 даёт конец вектора ускорения точки А, принадлежащей третьему звену (
даёт конец вектора ускорения точки А, принадлежащей третьему звену ( 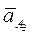 ).
).
Ускорение точки В3 определяем из пропорции (теорема о конгруэнтности)
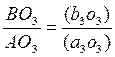
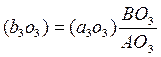
Направление углового ускорения третьего звена, величина которого равна 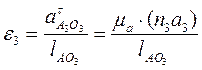 , определяется направлением тангенциального ускорения
, определяется направлением тангенциального ускорения 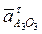 , приложенного (мысленно) в точке А.
, приложенного (мысленно) в точке А.
Строим план ускорений для второй присоединённой группы.
Векторные уравнения плана ускорений для второй присоединённой группы
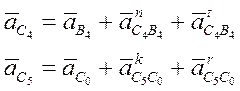
Ускорение точки В4 равно ускорению точки В3, и уже отложено. Вектор нормального ускорения, равный 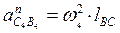 начинается в конце вектора
начинается в конце вектора 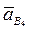 , параллелен отрезку СВ. Вектор тангенциального ускорения
, параллелен отрезку СВ. Вектор тангенциального ускорения 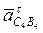 начинается в конце нормального
начинается в конце нормального 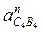 , перпендикулярен отрезку ВС и его направление пока неизвестно. Ускорение точки С0 известно, так как эта точка принадлежит стойке (оно равно нулю, т.е. вектор этого ускорения начинается и заканчивается в полюсе плана). Вектор ускорения Кориолиса
, перпендикулярен отрезку ВС и его направление пока неизвестно. Ускорение точки С0 известно, так как эта точка принадлежит стойке (оно равно нулю, т.е. вектор этого ускорения начинается и заканчивается в полюсе плана). Вектор ускорения Кориолиса 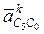 начинается в конце вектора С0 и определяется по выражению
начинается в конце вектора С0 и определяется по выражению 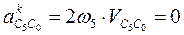 , так как ω5 = 0. Вектор радиального ускорения
, так как ω5 = 0. Вектор радиального ускорения 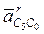 начинается в конце вектора Кориолиса, т.е. в полюсе плана ускорений, параллелен оси поступательной пары С и заканчивается в точке пересечения с тангенциальным ускорением
начинается в конце вектора Кориолиса, т.е. в полюсе плана ускорений, параллелен оси поступательной пары С и заканчивается в точке пересечения с тангенциальным ускорением 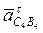 . Пересечение относительных ускорений
. Пересечение относительных ускорений 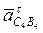 и
и 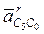 даёт конец вектора ускорения точки С, принадлежащей пятому звену (
даёт конец вектора ускорения точки С, принадлежащей пятому звену ( 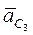 ). Направление углового ускорения четвёртого звена, величина которого равна
). Направление углового ускорения четвёртого звена, величина которого равна 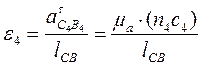 , определяется направлением тангенциального ускорения
, определяется направлением тангенциального ускорения 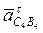 , приложенного (мысленно) в точке С.
, приложенного (мысленно) в точке С.
2. Кинематическое исследование аналитическим методом.
Если достоинством графического метода является абсолютная прозрачность, наглядность, то аналитический метод позволяет более точно определить кинематические параметры.
Впервые аналитические методы стал применять П.Л.Чебышев. Большой вклад в развитие этих методов внёс один из создателей теории точности механизмов, академик, Н.Г.Бруевич.
Сущность данного метода заключается в том, линейные и угловые координаты, скорости и ускорения звеньев определяются в виде аналитических выражений, которые содержат конечное число алгебраических или тригонометрических операций. Аналитические выражения определяют для координат, скоростей и ускорений характерных точек механизма, для которых необходимо количественное описание движения при проектировании и исследовании механизма.
|

.
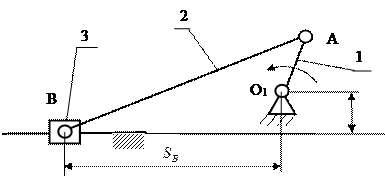
Н.Г.Бруевич заметил, что поскольку группа присоединяется к ведущему звену и стойке, то звенья группы вместе с ведущим звеном и стойкой образуют один или несколько замкнутых контуров. Это послужило основой для составления уравнений, позволяющих определить кинематические параметры механизма.

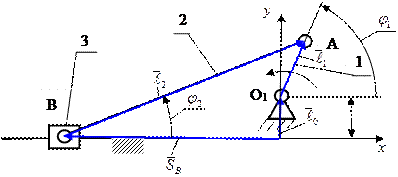 1. Составляем векторное
1. Составляем векторное
уравнение замкнутости
контура.
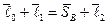
2. Выбираем систему координат и находим проекции векторов на оси выбранной системы координат.
а) Ось хвыбирается по оси поступательного движения ползуна в сторону оси вращательной кинематической пары (кп) О1. Ось y направляем так, чтобы проходила через ось вращательной кп О1. Принимаем положительное направление углов от оси х к оси у. Выбор положения и направление осей системы координат, так же как и выбор направления векторов, произвольное. Но от этого выбора зависит вид и сложность аналитических выражений. Чем они проще, тем легче по ним рассчитать, тем легче составить программу для расчёта.
б) Проекции векторов на оси системы координат
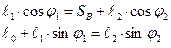
из второго уравнения можно определить φ2
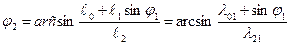
где
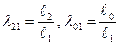
из первого уравнения определяем SB
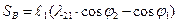
3. Полученные проекции векторов, дифференцируем по времени и определяем неизвестные скорости
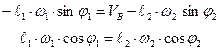
из второго уравнения выражаем ω2 и после преобразования получим
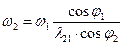
из первого уравнения после преобразования находим VB
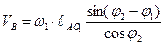
4. Полученные проекции векторов, дважды дифференцируем по времени и определяем неизвестные ускорения
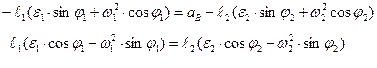
из второго уравнения можно определить ε2
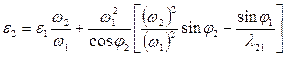
из первого уравнения можно определить аВ
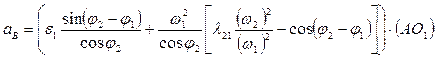
Все знаки угловых и линейных кинематических параметров, полученных в результате решения аналитических выражений, относятся к выбранной системе координат.
Используя, приведенную выше методику, можно вывести аналитические выражения для кинематических параметров механизмов с другими двухповодковыми группами, из которых состоит подавляющее большинство механизмов.
Дата добавления: 2020-02-05; просмотров: 1140;











