Вычисление определенного интеграла

1. Применение формулы Ньютона-Лейбница. Формула применяется во всех случаях, когда может быть найдена первообразная функция F(x) для подынтегральной функции f(x).

Пример.

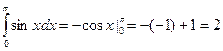
2. Интегрирование подстановкой (замена переменной).

Теорема. Пусть для вычисления интеграла 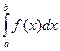от непрерывной функции была сделана подстановка х=φ(t), причем эта функция удовлетворяет следующим условиям: 1) функция х=φ(t) и ее производная х’=φ’(t) непрерывны при 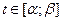; 2) отрезок 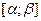является областью определения функции х=φ(t), а отрезок [a;b] является областью ее значений; 3) .

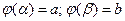Тогда справедлива следующая формула:

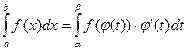
Пример.

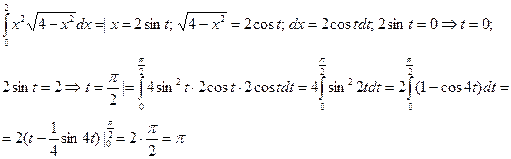
3. Интегрирование по частям.

Теорема. Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a;b], то имеет место формула:

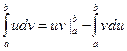
Пример.

1)

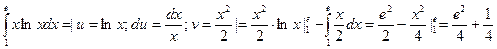
2)

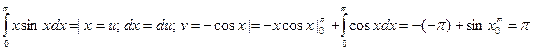
4. Интегрирование четных и нечетных функций в симметричных пределах.

Пусть задана функция 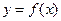непрерывная на отрезке [-a;a], симметричном относительно точки х=0. Тогда справедлива следующая формула:

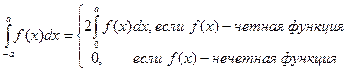
Пример.

1) 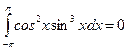; 2)

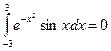
Лекция 11

Геометрические приложения определенного интеграла