Метод интегрирования подстановкой (замены переменной интегрирования)

Пусть требуется вычислить интеграл 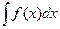, который не является табличным. Укажем два правила подстановки:

1) Независимую переменную х заменяют по формуле х=φ(t) (2.1), где φ(t) – дифференцируемая функция. Затем определяют dx=φ’(t)dt, а интеграл 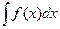приводят к виду 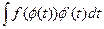. Цель подстановки будет достигнута, если окажется, что вычисление этого интеграла проще, чем исходного.

Теорема. Пусть функция х=φ(t) определена и дифференцируема на некотором множестве Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(х) имеет первообразную, то на множестве Т справедлива формула:

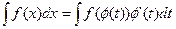(2.2)

Формула (2.2) называется формулой замены переменной в неопределенном интеграле.

В результате интегрирования получится функция независимой переменной t. Чтобы возвратиться к переменной x, надо из уравнения (2.1) определить t через x и подставить это значение в найденную функцию. Функция φ(t) должна иметь обратную для того, чтобы можно было определить t как функцию x.

2) Полагают, что 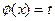(2.3). Эта подстановка отличается от предыдущей тем, что в (2.1) сама переменная x заменялась новой функцией φ(t), а здесь функция 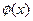заменяется новой переменной t. Из уравнения (2.3) находят dx. Делают подстановку, находят интеграл и переходят к первоначальной переменной x.

Примеры.

1)

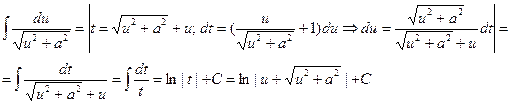
2)

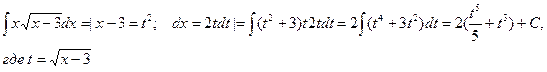
Лекция 3