Свойства определенного интеграла

Пусть задана непрерывная на отрезке [a;b] функция 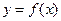(где a<b). Тогда справедливы следующие теоремы:

1. Постоянный множитель можно выносить за знак интеграла:

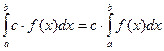, где с – некоторое число.

2. Определенный интеграл от алгебраической суммы конечного числа непрерывных на отрезке [a;b] функций равен алгебраической сумме определенных интегралов от слагаемых функций:

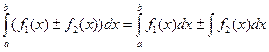
3. Если в определенном интеграле (где a<b) поменять местами пределы интегрирования, то определенный интеграл меняет знак на противоположный:

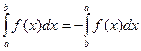
4. Если a<c<b, то 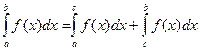. Это свойство называется аддитивностью определенного интеграла.

5. Теорема о среднем. Если функция 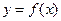непрерывна на отрезке [a;b], то внутри отрезка найдется такая точка с, что для нее справедлива следующая формула:

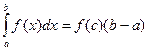
При f(x)≥0 теорема имеет простой геометрический смысл: значение определенного интеграла функции 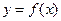на отрезке [a;b] равно площади прямоугольника с высотой f(c) и основанием (b-a).

6. Если функция f(x) сохраняет свой знак на отрезке [a;b], где a<b, то интеграл 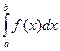имеет тот же знак, что и функция. Так, если f(x)≥0 на [a;b], то и .

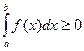7. Неравенство между непрерывными функциями на отрезке [a;b] можно интегрировать. Так, если 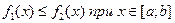, то .

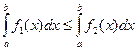Замечание: дифференцировать неравенства нельзя.

8. Оценка интеграла. Если m и М соответственно наименьшее и наибольшее значения функции y=f(x) на отрезке [a;b], то справедливо следующее двойное неравенство:

.

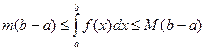Если f(x)≥0, то геометрический смысл этого свойства заключается в следующем: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых отрезок [a;b], а высоты равны m и М.

9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции: .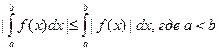

Так как 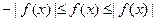, то 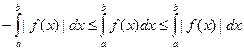. Отсюда и следует указанное неравенство .

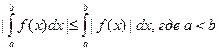10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом.

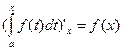
Так как по формуле Ньтона-Лейбница 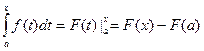, то

.

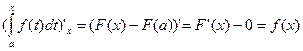Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

Лекция 10