Теорема Гюйгенса-Штейнера
Момент инерции тела относительно произвольной оси (I) равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела М на квадрат расстояния между осями:
I = Ic + Ma2, (9.9)
где а — расстояние между осями.
На рисунке 9.5 оси вращения перпендикулярны плоскости чертежа: через точку 0 проходит произвольная ось; параллельная ей ось проведена через центр масс тела — точку С. Расстояние между осями — а.
Выделим элемент тела массой Dmi. Его момент инерции относительно оси 0 равен:
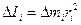 . (9.10)
. (9.10)
Как следует из рисунка 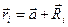 , откуда:
, откуда:
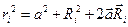 . (9.11)
. (9.11)
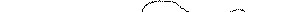
Рис. 9.5
Теперь момент инерции частицы Dmi (9.10) можно представить такой суммой:
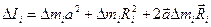 .
.
Для отыскания момента инерции всего тела, нужно сложить моменты инерции всех его частиц:
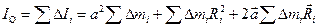 . (9.12)
. (9.12)
Здесь за знак суммы вынесена постоянная величина — расстояние между осями а. Первое слагаемое справа 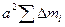 = Ма2, так как
= Ма2, так как 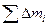 = М — масса тела. Второе слагаемое
= М — масса тела. Второе слагаемое 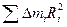 = IС — момент инерции тела, относительно оси, проходящей через центр масс. Третье слагаемое равно нулю, так как сумма
= IС — момент инерции тела, относительно оси, проходящей через центр масс. Третье слагаемое равно нулю, так как сумма 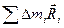 равна произведению массы тела на вектор
равна произведению массы тела на вектор 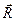 , проведённый от оси С к центру масс тела. Но ось С проходит через центр масс, поэтому
, проведённый от оси С к центру масс тела. Но ось С проходит через центр масс, поэтому 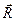 = 0 и
= 0 и 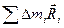 = М
= М 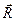 = 0.
= 0.
Собрав эти результаты в уравнение (9.12), получим выражение теоремы Гюйгенса-Штейнера:
IO = IC + Ma2.
Эта теорема значительно упрощает задачу вычисления моментов инерции.
Известен, например, момент инерции стержня относительно оси, проходящей через его центр масс (9.7):
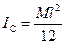 .
.
Воспользовавшись теоремой Гюйгенса-Штейнера, легко вычислим момент инерции этого же стержня относительно оси z’, проходящей, например, через край стержня (рис. 9.3):
Iz’ = Iz + Ma2, a = l/2.
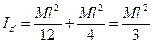 .
.
Это значение момента инерции совпадает с результатом (9.8), который был получен методом прямого интегрирования.
Дата добавления: 2021-01-11; просмотров: 514;











