Полная система уравнений, описывающая произвольное движение твердого тела. Условия его равновесия и покоя
Как уже отмечалось, произвольное движение твердого тела может быть представлено совокупностью двух простых движений: поступательного и вращательного. Причем деление произвольного движения на составляющие всегда неоднозначно.
Рассмотрим, например, качение цилиндра без проскальзывания по горизонтальной поверхности с постоянной скоростью V0 (рис. 10.1). Это движение можно представить, например, суммой таких двух движений:
1. Поступательного со скоростью центра масс V0
2. Вращения относительно оси, совпадающей с осью симметрии.

Рис. 10.1
Это вращение должно происходить с угловой скоростью:
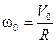 .
.
В этом случае точки на поверхности цилиндра будут двигаться со скоростью:
w0R = V0.
При сложении таких двух движений верхняя точка движется со скоростью VA = 2V0, вдвое превышающей скорость оси цилиндра V0. Скорость точек (В), касающихся горизонтальной поверхности будет равна нулю, что отвечает условию задачи: качание происходит без проскальзывания(VВ = 0).
То же самое движение может быть представлено и совершенно по-другому. В этом и заключается неоднозначность разделения сложного движения на составляющие.
Например, качание этого же цилиндра можно рассматривать как нескончаемая цепь поворотов цилиндра относительно оси, совпадающей с образующей цилиндра В, лежащей на горизонтальной поверхности (рис. 10.2). Это — мгновенная ось вращения, так как в процессе качания она движется и по поверхности цилиндра и по горизонтальной поверхности. Это вращение цилиндра относительно мгновенной оси должно происходить с угловой скоростью:
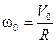 .
.

Рис. 10.2
Тогда скорость поступательного движения цилиндра (скорость его оси) будет отвечать условию задачи:
w0R = V0.
При этом мгновенная скорость верхней точки цилиндра, как мы уже знаем, будет вдвое выше:
VA = w02R = 2w0R = 2V0.
Если, в общем случае, представлять произвольное движение твёрдого тела суммой поступательного и вращательного, то каждое из этих движений описывается своим законом. Таким законом для поступательного движения является теорема о движении центра масс:
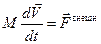 , (10.1)
, (10.1)
а для вращательного движения — уравнение моментов:
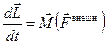 . (10.2)
. (10.2)
Система этих двух векторных уравнений при проецировании их на оси декартовой системы координат переходит в систему шести скалярных уравнений:
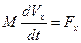 ,
, 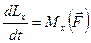 ,
,
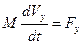 ,
, 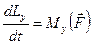 ,
,
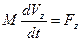 ,
, 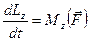 .
.
Если на рассматриваемое тело не действуют внешние силы 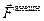 = 0, то и момент внешних сил отсутствует
= 0, то и момент внешних сил отсутствует 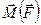 = 0. Это условие отвечает равновесию тела. В этом состоянии тело может покоиться (V = 0, w = 0), либо двигаться с постоянной линейной и угловой скоростями (V = сonst., w = сonst.). При этом импульс тела и момент импульса сохраняют своё значение
= 0. Это условие отвечает равновесию тела. В этом состоянии тело может покоиться (V = 0, w = 0), либо двигаться с постоянной линейной и угловой скоростями (V = сonst., w = сonst.). При этом импульс тела и момент импульса сохраняют своё значение
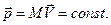 ,
, 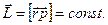
Твёрдое тело будет находиться в покое, если для него выполняются условия равновесия:
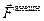 = 0;
= 0;
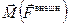 = 0,
= 0,
и, кроме того, начальные скорости тела — линейная и угловая равны нулю:
V(0) = V0 = 0;
w(0) = w0 = 0.
Это означает, что тело, находящееся в покое, не покинет это состояние, если оно находится в равновесии.
Подводя итог, сформулируем основные выводы:
Полная система уравнений, описывающая произвольное движение твёрдого тела:
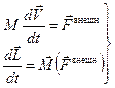 . (10.3)
. (10.3)
Условия равновесия твёрдого тела:
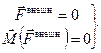 . (10.4)
. (10.4)
Условия покоя:
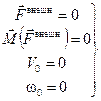 . (10.5)
. (10.5)
Дата добавления: 2021-01-11; просмотров: 441;











