Скатывание тел с наклонной плоскости

С тем, чтобы проиллюстрировать применение законов динамики твёрдого тела, решим задачу о скатывании цилиндра с наклонной плоскости (рис. 10.5).

Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с наклонной плоскости. Угол наклона плоскости — a, а высота Н (Н » R). Начальная скорость цилиндра равна нулю. Определим время скатывания — Т и скорость центра масс цилиндра у основания наклонной плоскости.

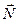При качении цилиндра на него действуют три силы: сила тяжести , упругая сила реакции опоры и сила трения покоя 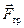(ведь качение без проскальзывания!).

Представим это движение суммой двух движений: поступательного со скоростью V_C, с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью w.

. (10.9)

Рис. 10.5

Эта связь скоростей поступательного и вращательного движений следует из условия «движение без проскальзывания».

Продифференцировав уравнение (10.9) по времени, получим соотношение углового и линейного ускорений цилиндра:

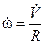, то есть .

Воспользовавшись теоремой о движении точки центра масс, опишем поступательное движение цилиндра:

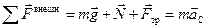. (10.10)

Для описания вращения воспользуемся основным уравнением динамики вращательного движения:

M_C = I_C × e. (10.11)

Спроецировав уравнение (10.10) на направления осей x и y, получим два скалярных уравнения:

x: mgSina – F_тр = ma_C; (10.12)

y: N – mgсosa = 0. (10.13)

Обратимся теперь к уравнению (10.11). Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:

.

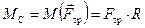Момент инерции сплошного цилиндра относительно его оси равен (см. лекцию №9):

.

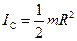Учитывая всё это, уравнение (10.11) перепишем так:

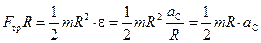. (10.14)

Решая совместно уравнения (10.12) и (10.14), получим следующие значения неизвестных величин:

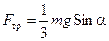; (10.15)

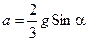. (10.16)

Из уравнения (10.15) следует, что с увеличением угла наклона a должна возрастать и сила трения покоя F_тр. Но, как известно, её рост ограничен предельным значением:

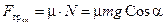. (10.17)

Так как сила трения покоя (10.15) не может превышать предельного значения (10.17), то должно выполняться неравенство:

⅓mgSina ≤ mmgCosa.

Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол a не превзойдёт значения a_пред:

a_пред = arctg3m.

Здесь m — коэффициент трения цилиндра по плоскости.

Линейное ускорение цилиндра (10.16) величина неизменная, следовательно, поступательное движение цилиндра равноускоренное. При таком движении без начальной скорости цилиндр достигнет основания наклонной плоскости за время:

.

Здесь: l = 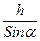— длина плоскости;

a = 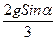, (см.10.16).

Значит, время скатывания:

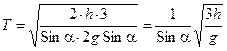. (10.18)

Вычислим конечную скорость поступательного движения оси цилиндра:

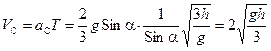. (10.19)

Заметим, что эту задачу можно решить проще, воспользовавшись законом сохранения механической энергии.

В системе, правда, присутствует сила трения, но её работа равна нулю, поскольку точка приложения этой силы в процессе спуска остаётся неподвижной: ведь движение происходит без проскальзывания. Раз нет работы силы трения, механическая энергия системы не меняется.

Рассмотрим энергию цилиндра в начальный момент — на высоте h и в конце спуска. Полная энергия цилиндра в этих положениях одинакова:

.

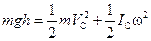Вспомним, что и 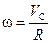. Тогда уравнение закона сохранения энергии можно переписать так:

.

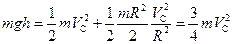Отсюда легко найдём конечную скорость цилиндра:

,

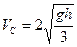которая блестяще подтверждает полученный нами ранее результат (10.19).