Базисы и размерность пространства.

Определение(уже рассматривали ранее).

1) Максимальная линейно независимая подсистема данной системы называется базисом системы, количество векторов в ней - рангом системы.

2) Максимальная линейно независимая система элементов линейного пространства называется базисом пространства, количество векторов в ней - размерностью пространства.

Определение.Если пространство имеет хотя бы один конечный базис, оно называется конечномерным.

Теорема 1. Все базисы конечномерного линейного пространства 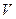состоят из одного и того же конечного числа элементов.

Доказательство.

Пусть 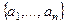(1) один базис, 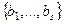(2) другой базис.

Если (2) базис, значит, любой вектор из системы (1) можно выразить через него, т.е. 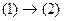. При этом (1) тоже базис, значит, 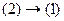. Тогда это эквивалентные системы 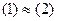, а согласно следствию (в конце прошлого §) они состоят из одного и того же количества векторов. Если есть хотя бы один конечный базис, он эквивалентен любому другому базису, и тот тоже не может содержать бесконечное количество векторов.

Определение.Количество векторов в любом базисе конечномерного пространства 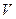называется размерностью пространства и обозначается .

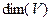Если пространство n-мерно, то всякая система, состоящая из 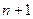вектора, линейно зависима (очевидно, следует из определений выше).

В плоскости любые 3 вектора образуют ЛЗС, в пространстве 4 вектора, на прямой любые 2 вектора.

Лекция 11. 14.12.2020.

Теорема 2(о выражении векторов через базис).

Всякий вектор конечномерного линейного пространства линейно выражается через любой базис этого пространства, притом единственным образом.

Доказательство.Пусть 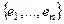некоторый базис, значит, это максимальная линейно независимая система, поэтому при добавлении любого вектора 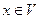она становится линейно зависимой:

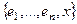ЛЗС. Тогда при каком-то ненулевом наборе коэффициентов 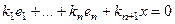. При этом 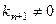, иначе система 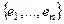была бы ЛЗС. Тогда можно перенести направо все слагаемые, кроме последнего, и поделить на коэффициент :

, .

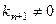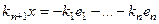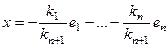Итак, произвольный вектор 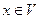можно выразить через базис.

Единственность. Пусть существуют 2 разных выражения через базис:

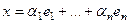и .

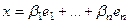Составим разность: .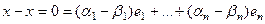

Если хоть какие-то коэффициенты были бы отличны, то система 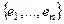была бы линейно зависима, что противоречит тому, что она является базисом.

Следствие.Всякая линейно-независимая система из n векторов

n-мерного пространства является базисом.

В плоскости любые 2 неколлинеарных вектора, в пространстве любые 3 некомпланарных вектора образуют базис.

Определение.Коэффициенты линейной комбинации, с помощью которых вектор представлен в виде комбинации векторов базиса, называются координатамиэтого вектора относительного данного базиса.