Алгоритм ортогонализации Грама-Шмидта
Пусть дана не ортогональная система векторов 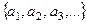 . Первый вектор возьмём из старой системы без изменения
. Первый вектор возьмём из старой системы без изменения 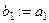 . Теперь мы должны найти второй вектор
. Теперь мы должны найти второй вектор 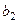 , так чтобы он был ортогонален
, так чтобы он был ортогонален 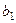 . К вектору
. К вектору 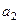 нужно прибавить
нужно прибавить 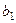 , домноженный на какой-то коэффициент, чтобы подвинуть конец вектора
, домноженный на какой-то коэффициент, чтобы подвинуть конец вектора 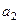 таким образом, чтобы новый изменённый вектор стал ортогонален
таким образом, чтобы новый изменённый вектор стал ортогонален 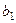 . Чертёж:
. Чертёж:
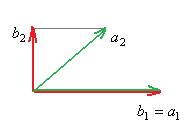
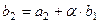 , причём
, причём 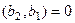 . Тогда
. Тогда
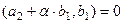 то есть
то есть 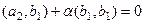 , тогда
, тогда 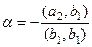 .
.
Таким образом, 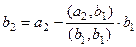 .
.
Далее, рассмотрим вектор 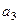 , он также изначально может быть не ортогонален векторам
, он также изначально может быть не ортогонален векторам 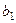 и
и 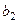 , необходимо прибавить к нему линейную комбинацию, состоящую из них. Ищем в виде
, необходимо прибавить к нему линейную комбинацию, состоящую из них. Ищем в виде 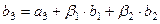 , причём так, чтобы было выполнено
, причём так, чтобы было выполнено 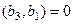 и
и 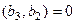 .
.
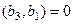
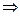
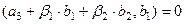
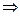
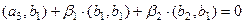 , причём
, причём 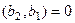 так как эта часть системы уже была построена как ортогональная (на прошлом шаге).
так как эта часть системы уже была построена как ортогональная (на прошлом шаге).
Тогда 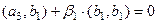
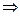
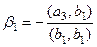 .
.
Аналогично 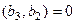 означает, что
означает, что 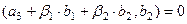
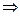
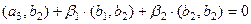
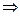
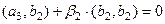
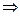
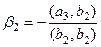 .
.
Итак, 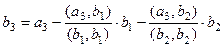 . Теперь все 3 вектора
. Теперь все 3 вектора 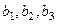 ортогональны между собой. Аналогично этот процесс можно продолжить и для n векторов.
ортогональны между собой. Аналогично этот процесс можно продолжить и для n векторов.
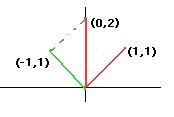
Пример.Ортогонализовать систему векторов (1,1), (0,2).
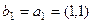 ,
, 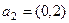 .
.
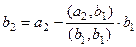 .
. 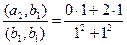 =
= 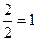 .
.
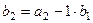 =
= 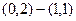 =
= 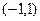
Лекция 14. 26.12.2020.
Ортогональные матрицы.Пусть новый базис также ортонормированный, тогда матрица перехода обладает следующими свойствами:
1) сумма квадратов всех элементов любого столбца равна 1.
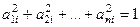
2) скалярное произведение двух различных векторов-столбцов = 0.
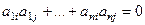 .
.
Такая матрица называется ортогональной матрицей.
Лемма.Если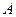 ортогональная матрица, то
ортогональная матрица, то 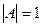 .
.
(Объём параллелепипеда, построенного на ортонормированной системе, равен 1).
Теорема.Если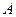 ортогональная матрица, то
ортогональная матрица, то 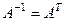 .
.
Доказательство.Умножим 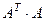
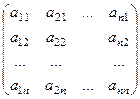
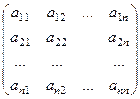 =
= 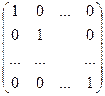
Строка в первой матрице, это бывший столбец (до транспонирования). Таким образом, умножая  -ю строку на
-ю строку на 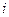 -й столбец, мы получаем
-й столбец, мы получаем 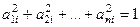 . А если
. А если 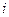 -ю строку умножаем на
-ю строку умножаем на 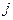 -й столбец, то это то же самое, что скалярно умножить друг на друга
-й столбец, то это то же самое, что скалярно умножить друг на друга 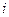 -й столбец на
-й столбец на 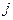 -й столбец в исходной матрице, а это
-й столбец в исходной матрице, а это 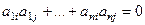 .
.
Тогда 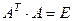 , а значит, транспонированная матрица это и есть обратная, что и требовалось доказать.
, а значит, транспонированная матрица это и есть обратная, что и требовалось доказать.
Примером такой матрицы является матрица оператора поворота: 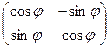 , здесь можно устно проверить, что сумма квадратов элементов каждого столбца равна 1 (по основному тригонометрическому тождеству), а скалярное произведение 1-го и 2-го столбцов 0. Чтобы найти обратную к ней матрицу, достаточно лишь транспонировать её.
, здесь можно устно проверить, что сумма квадратов элементов каждого столбца равна 1 (по основному тригонометрическому тождеству), а скалярное произведение 1-го и 2-го столбцов 0. Чтобы найти обратную к ней матрицу, достаточно лишь транспонировать её.
Ещё примеры ортогональных матриц.
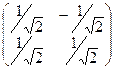 ,
, 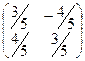 .
.
Дата добавления: 2021-01-11; просмотров: 835;











