Изоморфизм линейных пространств.

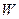Определение.Пусть и – линейные пространства над полем 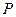. Отображение 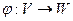называется изоморфизмом, если оно взаимно однозначно и выполняются условия:

1) ,

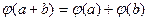
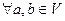2) .

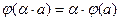
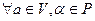Если существует какой-либо изоморфизм 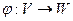, то пространства называются изоморфными, если не существует, то не изоморфными.

Теорема 1.(об изоморфизме линейного пространства пространству векторов-строк).

Пусть – линейное пространство размерности n над полем .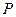

Тогда 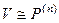, где 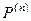– пространство векторов-строк длины n над полем .

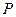Доказательство.Пусть 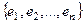– какой-либо базис пространства . Определим изоморфизм 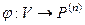таким образом:

если 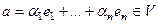, то .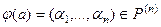

Это отображение взаимно однозначно. Пусть .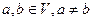

, .

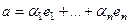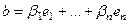Тогда найдётся хотя бы одна 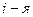координата, что 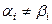. Тогда они не совпадают и в 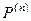. Итак, отображение инъективно. Сюръективность. Для 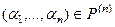найдётся вектор .

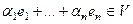Проверим сохранение операций. ,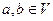

, .

.

= = .

= = .

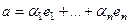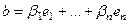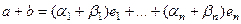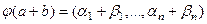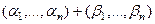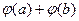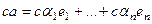
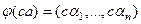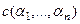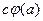Итак, .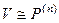

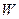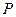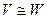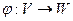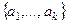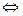
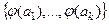Теорема 2.Пусть и – линейные пространства над полем . , изоморфизм. Система ЛЗС в

ЛЗС в .

Доказательство. 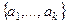ЛЗС в означает, что 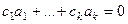, тогда 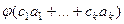= 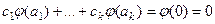, то есть система 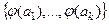ЛЗС в .

Обратно, пусть 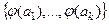ЛЗС, .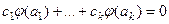

Поскольку 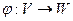изоморфизм, то существует обратное отображение 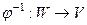, тоже являющееся изоморфизмом. Применим 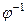к сумме 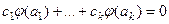, получим .

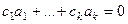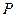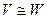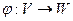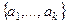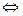
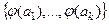Следствие.Пусть и – линейные пространства над полем . , изоморфизм. Система ЛНС в

ЛНС в .

Теорема 3.(Об изоморфизме линейных пространств).

Пусть и – линейные пространства над полем .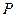

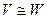
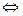
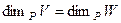(они имеют одинаковую размерность).

Доказательство.

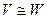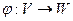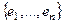Необходимость. Пусть , изоморфизм. Возьмём в некоторый базис . Докажем, что система 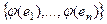образует базис в . По предыдущему следствию, она ЛНС. Тогда уже, как минимум, 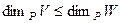, так как в есть ЛНС из n элементов. Покажем, что размерность не больше или равна, а именно равна размерности . Пусть размерность больше, то есть 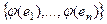ЛНС, но не базис. Тогда там есть ЛНС из 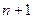векторов, 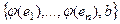. Так как 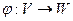взаимно однозначное отображение, то 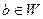является образом некоторого элемента .

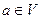Тогда 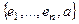ЛНС, но это невозможно, так как 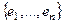базис (максимальная линейно независимая система). Тогда 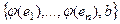ЛЗС для всякого 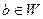, т.е. 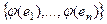базис, и следовательно, .

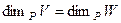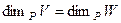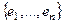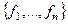Достаточность. Пусть . Зафиксируем какие-то два базиса: в и в .

Построим изоморфизм так: если 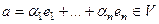, то положим 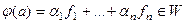, то есть 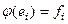. Это действительно взаимно однозначное отображение. Если было бы не так, то например 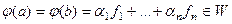, тогда было бы

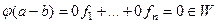, т.е. ненулевому вектору поставили бы в соответствие (0,...,0), что противоречит построению .

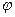Сохранение операций:

1) =

=

= .

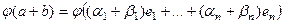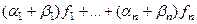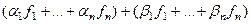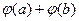2) = =

= .

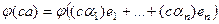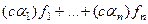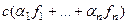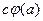Лекция 12. 19.12.2020.

Подпространства.

Определение.Пусть – линейное пространство над полем .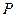

Непустое подмножество его элементов, , называется подпространством пространства , если оно само является линейным пространством относительно операций, введённых для .

Тривиальные подпространства: 0 и . Остальные подпространства называются собственными.

Обозначение: .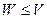

Вовсе не любое подмножество является подпространством. Например, если рассматривать все радиус-векторы, концы которых лежат на прямой, не проходящей через начало координат, то не получается подпространство. Сумма векторов (находится по правилу параллелограмма) оказывается не на этой прямой, впрочем, даже .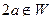

.

Теорема 1. (Критерий подпространства).

Пусть – линейное пространство над полем 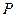, – его непустое подмножество. является подпространством в 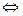выполнены условия: 1)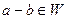 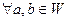2) .

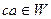
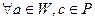Доказательство.

Необходимость: если подпространство, то оно во-первых является подгруппой как абелева группа, и тогда 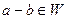, во-вторых, 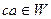так как оно само является линейным пространством.

Достаточность. Пусть выполнено:

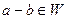
1) 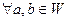2) .

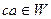
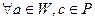Из 1) следует, что абелева группа (по критерию подгруппы).

Из 2) следует, что операция внешнего умножения порождает элемент снова из . Таким образом, образует линейное пространство.

Теорема 2. Пусть 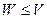(подпространство). Тогда .

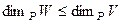Если 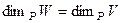то .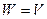

Доказательство.1) Обозначим 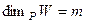, 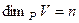. Допустим, что 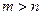. Тогда существует линейно независимая система 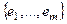в пространстве . Однако все эти векторы одновременно с тем находятся и в пространстве . Тогда получалось бы, что в существует ЛНС из более чем 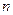векторов, хотя его размерность равна 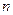. Противоречие.

2) Допустим, 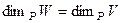. Тогда базис в состоит из 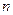векторов, и одновременно является базисом пространства . Если 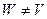, то должен был бы существовать вектор 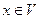, который нельзя выразить через базис пространства . Но базис пространства является также базисом пространства , поэтому такое невозможно.

Определение.Линейной оболочкой системы векторов 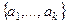пространства называется множество всевозможных их линейных комбинаций: .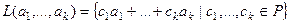

По критерию подпространства, линейная оболочка является подпространством. Это подпространство, порождённое системой . . . . . (…) *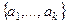

Если эти векторы образуют ЛНС, то 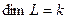, если ЛЗС, то .

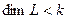Следствие.Если 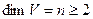, то в существуют подпространства всех размерностей от 1 до .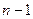

Действительно, 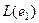одномерно, 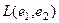двумерно и т.д.