Пересечение и сумма подпространств.

Определение.Пусть .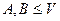

1) 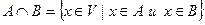называется пересечением подпространств

2) 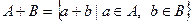называется суммой подпространств.

Теорема 3. Пересечение и сумма подпространств являются подпространствами.

Доказательство.

1) Если 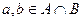, то одновременно 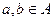, 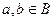. Так как 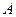подпространство, то 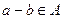, 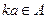. При этом 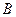тоже подпространство, так что 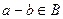, 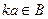. Таким образом,

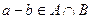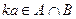, , а значит, по критерию подпространства,

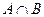подпространство.

2) Если 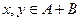, то каждый из этих элементов представляется в виде: 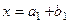, , 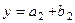где , .

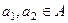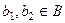В таком случае 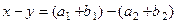= 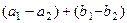, каждое из 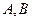подпространство, значит, 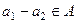, , 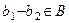то есть .

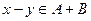Если 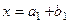, то .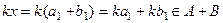

Теорема 4. О размерности суммы подпространств.

Пусть 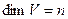, 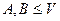. Тогда: .

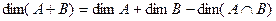Доказательство.Пусть , , .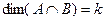

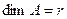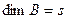Выберем базис 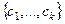пространства 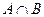. Все эти векторы образуют ЛНС и принадлежат 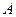. Тогда, по теореме о продолжении базиса, можно найти такие векторы 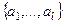,что система

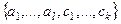является базисом в 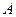. Но так как размерность 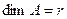, то .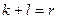

Аналогично, все векторы 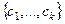лежат в 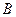, значит, и там можно достроить до базиса: 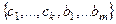. Но так как размерность 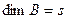, то .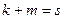

, .

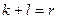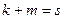
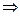
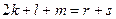
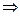
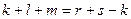Есть 3 системы:

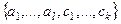(1) базис в ,

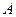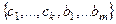(2) базис в ,

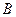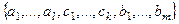(3) возможно, базис в 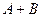. (докажем).

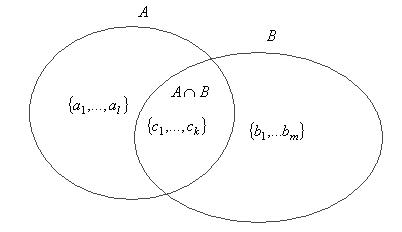
Докажем, что система 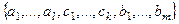является базисом в пространстве .

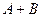1) Докажем, что она ЛНС. Предположим, что она ЛЗС, т.е.

,

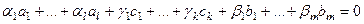где вектор 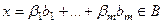. Но тогда он равен

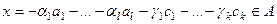. Значит, этот вектор принадлежит пересечению 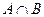. Но тогда в его выражении отсутствуют слагаемые 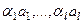, т.е. .

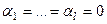Тогда 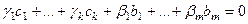. Но система 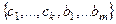- базис в 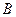, т.е. ЛНС, тогда и 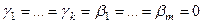, т.е. вообще все эти коэффициенты 0. То есть, эта система ЛНС.

2) Докажем, что любой вектор 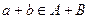, где 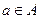, 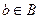линейно выражается через эту систему (3).

Вектор 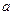линейно выражается через (1), при этом (1) входит в (3), значит, 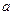выражается через (3).

Вектор 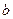линейно выражается через (2), при этом (2) входит в (3), значит, 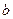выражается через (3). 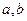выражаются через (3), значит,

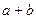выражается через (3).

Итак, (3) ЛНС и через неё выражается любой вектор, значит, это базис. Вспомним, что количество векторов в нём 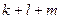и равно

= .

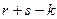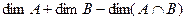- - - Перерыв - - -

Определениепрямой суммы.

Сумма подпространств 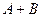называется прямой суммой, если представление любого вектора, принадлежащего 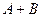, в виде суммы 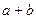является однозначным.

Обозначение: .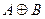

Теорема 5. (о прямой сумме подпространств).

Сумма 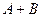является прямой суммой .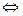

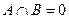Доказательство.

Необходимость. Пусть сумма является прямой суммой, но 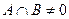. Тогда некоторый ненулевой вектор .

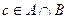Пусть 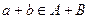. При этом представление вектора неоднозначно, например, он также представим в виде 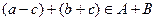, где первая компонента 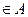, вторая 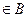. Действительно, ведь 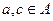, , 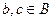поэтому , .

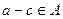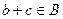Достаточность. Пусть 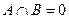, но при этом есть 2 представления вектора: 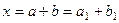, где 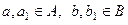. Но тогда вектор

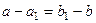принадлежит 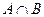, однако 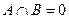, поэтому 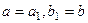и представление единственно.

Теорема 6.Сумма подпространств является прямой суммой тогда и только тогда, когда .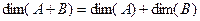

Доказательство.Необходимость.

По теореме 4, 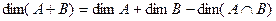. По прошлой теореме 5, если сумма прямая, то 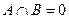. Тогда 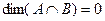, и

.

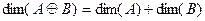Достаточность. Так как 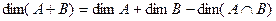, то 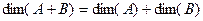означало бы 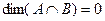, т.е. это 0-мерное пространство, т.е. 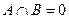, тогда по Т.5. сумма прямая.

Пример. Всякое векторное пространство является прямой суммой своих подпространств, равных линейным оболочкам ,..., .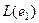

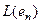Упражнение.Сколько векторов содержит линейное пространство векторов-строк длины n над полем 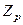? (p простое число).

Если каждая координата имеет вид 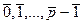. Если 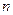координат, то общее число векторов .

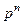Например, над полем , = .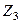

, ,

, ,

, ,

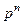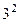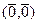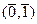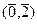
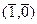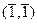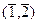
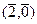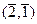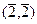
Линейная зависимость над конечным полем.

Коллинеарные векторы 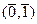+ 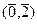= = 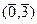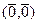, впрочем, они остаются ЛЗ и по старой причине: = .

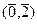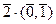Однако, здесь образуют ЛЗС и векторы , :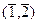

+ = = .

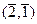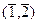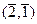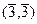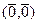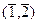и 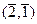коллинеарны над :

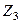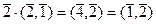
При этом определитель:

.

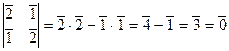Рассмотрим векторы 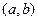, 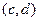. Их линейная комбинация 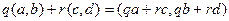, где .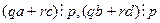

.

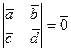В этом случае для линейной комбинации строк матрицы, где одна строка матрицы умножается на 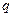, другая на 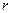, все координаты делятся на 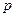, т.е. вектор 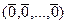. Строки ЛЗ, определитель 0.

Пример прямой суммы не векторных подпространств.

Упражнение.Доказать, что 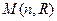– линейное пространство всех матриц порядка n над полем 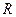, является прямой суммой двух подпространств: 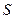всех симметрических матриц и 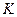– всех кососимметрических матриц. .

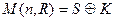Рассмотрим матрицы 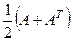и .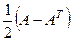

1) Матрица 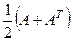является симметрической: на месте 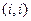останутся 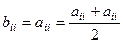, на прочих местах: .

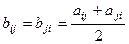2) Матрица 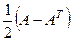является кососимметрической, , .

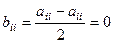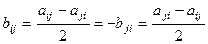При этом = .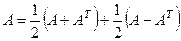

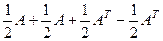Например, = + .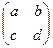

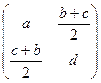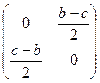Лекция 13. 21.12.2020.