Евклидовы и метрические пространства.
Определение. Говорят, что в линейном пространстве  над полем
над полем 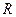 задано скалярное произведение, если задана функция
задано скалярное произведение, если задана функция 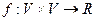 , то есть каждой паре векторов можно однозначно поставить в соответствие число, обозначаемое
, то есть каждой паре векторов можно однозначно поставить в соответствие число, обозначаемое 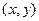 , причём выполнены условия:
, причём выполнены условия:
1) 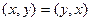
2) 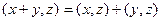 ,
, 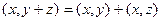
3) 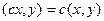 ,
, 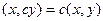
4) 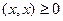 , причём
, причём 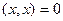
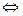
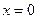 .
.
Линейное пространство называется евклидовым, если в нём определено скалярное произведение.
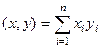
Определение.Модулем, или нормой вектора 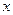 называется число
называется число 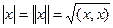 .
.
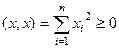 именно поэтому применяется понятие «нормировать вектор», что означает поделить на его модуль.
именно поэтому применяется понятие «нормировать вектор», что означает поделить на его модуль.
Теорема (неравенство Коши-Буняковского)
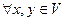 :
: 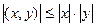 .
.
Эквивалентное равенство: 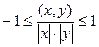 .
.
Доказательство. Рассмотрим скалярное произведение 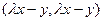 . Так как здесь умножается один и тот же вектор на себя, то оно неотрицательно:
. Так как здесь умножается один и тот же вектор на себя, то оно неотрицательно: 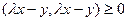 . По свойствам скалярного произведения, раскроем скобки:
. По свойствам скалярного произведения, раскроем скобки:
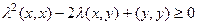
А теперь рассмотрим это выражение как неравенство с квадратичным трёхчленом относительно переменной 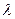 . Для каждых конкретных векторов
. Для каждых конкретных векторов 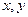 то это неравенство приобретает вид:
то это неравенство приобретает вид: 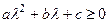 , где
, где 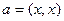 ,
, 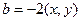
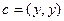 . Если выражение больше при равно 0, то значит, для самого квадратичного уравнения нет корней или всего 1 корень, но не 2 корня. То есть, дискриминант меньше или равен 0. Тогда
. Если выражение больше при равно 0, то значит, для самого квадратичного уравнения нет корней или всего 1 корень, но не 2 корня. То есть, дискриминант меньше или равен 0. Тогда 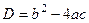 =
= 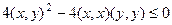 , тогда
, тогда
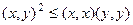
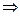
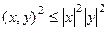
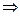
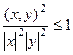 .
.
Извлечём корень и получим 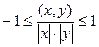 .
.
В связи с тем, что выполняется неравенство Коши-Буняковского, можно ввести понятие угла между векторами:
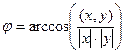
В связи с этим, основное свойство скалярного произведения
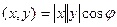 .
.
Тоже его сегодня докажем, пока не совсем очевидно, ведь могли определить функцию угла также и в виде 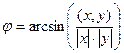 .
.
Определение.Два вектора 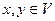 называются ортогональными, если
называются ортогональными, если 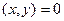 .
.
Теорема.Всякая система ненулевых попарно ортогональных векторов линейно независима.
Доказательство.
Пусть 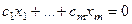 . Скалярно умножим равенство на
. Скалярно умножим равенство на 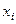 .
.
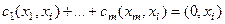 . Справа очевидно 0, а среди всех слагаемых ненулевое только
. Справа очевидно 0, а среди всех слагаемых ненулевое только 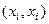 , т.к.
, т.к. 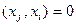
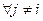 .
.
Тогда 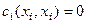 , но
, но 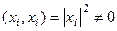 , поэтому
, поэтому 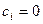 .
.
Указанное верно для любого 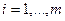 , все коэффициенты равны 0, то есть система ЛНС.
, все коэффициенты равны 0, то есть система ЛНС.
Определение.Базис пространства 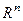 называется ортогональным, если все его векторы попарно ортогональны. Если при этом их длины равны 1, то базис называется ортонормированным.
называется ортогональным, если все его векторы попарно ортогональны. Если при этом их длины равны 1, то базис называется ортонормированным.
Билинейная форма.
Рассмотрим скалярное произведение вида 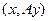 , где А - матрица порядка n. Произведение квадратной матрицы на столбец
, где А - матрица порядка n. Произведение квадратной матрицы на столбец 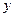 это вектор-столбец, затем его скалярно умножаем на вектор
это вектор-столбец, затем его скалярно умножаем на вектор 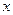 , в итоге получится число. Таким образом,
, в итоге получится число. Таким образом, 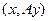 это некоторая скалярная функция от двух векторов. Она линейна по каждому аргументу: если на 1 или 2 месте сумма векторов, то результат тоже представляется в виде суммы. Обозначим
это некоторая скалярная функция от двух векторов. Она линейна по каждому аргументу: если на 1 или 2 месте сумма векторов, то результат тоже представляется в виде суммы. Обозначим 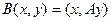 и назовём эту функцию билинейной формой. Подробнее при n=2 :
и назовём эту функцию билинейной формой. Подробнее при n=2 :
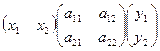 =
= 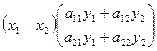 =
= 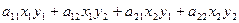 .
.
При произвольном n: 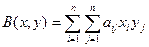 здесь n2 слагаемых.
здесь n2 слагаемых.
Скалярное произведение можно задать как умножение вида 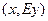 : : 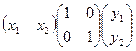 = = 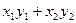 . Это частный случай билинейной формы. . Это частный случай билинейной формы.
|
Теперь рассмотрим такой случай. Пусть билинейная форма вычисляется от 2 одинаковых векторов, 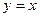 . Обозначим
. Обозначим 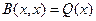 и назовём эту функцию, отображающую один вектор в число, квадратичной формой.
и назовём эту функцию, отображающую один вектор в число, квадратичной формой.
Квадратичная форма задаётся через скалярное произведение так: 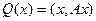 .
.
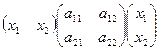 =
= 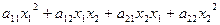 .
.
Например, матрица 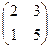 задаёт такую квадратичную форму:
задаёт такую квадратичную форму:
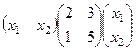 =
= 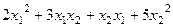 =
= 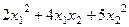 .
.
Очевидно, 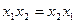 , то есть эта группа из двух слагаемых
, то есть эта группа из двух слагаемых 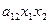 и
и 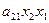 может быть объединена. Коэффициенты
может быть объединена. Коэффициенты 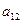 и
и 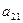 распределить поровну. Так,
распределить поровну. Так, 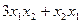 это то же самое, что
это то же самое, что 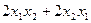 . Но ведь тогда матрицу квадратичной формы можно сделать симметричной, перераспределить эквивалентные элементы с сохранением их суммы. Таким образом, квадратичную форму всегда можно задать симметричной матрицей. Эта же самая квадратичная форма может быть задана и такой матрицей:
. Но ведь тогда матрицу квадратичной формы можно сделать симметричной, перераспределить эквивалентные элементы с сохранением их суммы. Таким образом, квадратичную форму всегда можно задать симметричной матрицей. Эта же самая квадратичная форма может быть задана и такой матрицей: 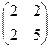 .
.
Пример.Построить матрицу квадратичной формы.
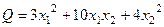 .
.
Решение.Распределим поровну коэффициенты:
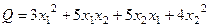 . Каждый коэффициент, стоящий при
. Каждый коэффициент, стоящий при 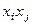 , запишем на место
, запишем на место 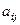 .
.
Ответ: матрица: 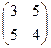 .
.
Если матрица Е, то квадратичная форма: 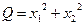 .
.
- - - Перерыв - - -
Вернёмся к свойствам скалярного произведения.
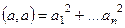
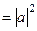 , что можно представить в виде:
, что можно представить в виде:
 .
.
Скалярное произведение обладает важным свойством:
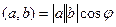 .
.
(Скалярное произведение равно произведению модулей векторов на косинус угла между ними).
Докажемэто свойство. Сначала расположим первый вектор на оси Ох, пусть его координаты 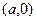 , второй вектор
, второй вектор 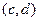 . Тогда их скалярное произведение равно
. Тогда их скалярное произведение равно 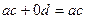 . С другой стороны, произведение модулей на косинус угла:
. С другой стороны, произведение модулей на косинус угла:
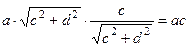 .
.
Линейный оператор поворота.В следующем семестре будут изучаться отображения линейных пространств. Однако коротко рассмотрим определения уже сейчас, это необходимо для доказательства свойств скалярного произведения. Вспомним, что при умножении квадратной матрицы на столбец, один вектор преобразуется в другой. Получается, что квадратная матрица задаёт некоторое отображение, т.е. выступает в роли функции.
Определение. Отображение 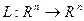 называется линейным отображением (синоним: линейный оператор) если выполнены условия: 1)
называется линейным отображением (синоним: линейный оператор) если выполнены условия: 1) 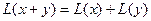 2)
2) 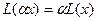 .
.
Либо вместо этих двух условий можно рассматривать одно (экв.):
3) 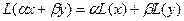 .
.
Умножение квадратной матрицы на вектор удовлетворяет свойствам линейности, в силу свойств умножения матриц.
Из определения напрямую следует, что всякое линейное отображение полностью определяется образами базисных векторов: 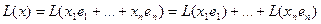 =
= 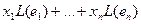 .
.
Образ вектора x в итоге зависит от координат вектора x и от образов базисных векторов, то есть линейный оператор однозначно задаётся образами базисных векторов.
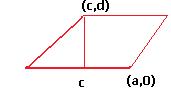
Матрица оператора поворота. Найдём матрицу оператора поворота на произвольный угол 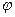 . Рассмотрим, куда отобразится базис.
. Рассмотрим, куда отобразится базис.
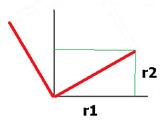
Расстояния r1 и r2 здесь равны 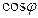 и
и 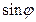 . Красным показаны образы базисных векторов. Получаем матрицу
. Красным показаны образы базисных векторов. Получаем матрицу 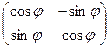 .
.
При 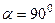 получится
получится 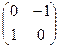 Действие оператора на любой вектор задаётся матрицей так:
Действие оператора на любой вектор задаётся матрицей так: 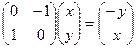 - любой вектор поворачивается на 90 градусов.
- любой вектор поворачивается на 90 градусов.
При 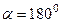 матрица будет иметь вид
матрица будет иметь вид 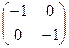 , и действительно, умножение на такую матрицу переводит любой вектор
, и действительно, умножение на такую матрицу переводит любой вектор 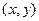 в
в 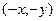 , а при повороте на
, а при повороте на 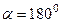 каждый вектор как раз и должен повернуться и стать противоположным исходному.
каждый вектор как раз и должен повернуться и стать противоположным исходному.
Теперь с помощью линейного оператора поворота плоскости докажем, что скалярное произведение не изменяется при повороте.
Рассмотрим векторы 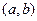 и
и 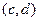 . Их скалярное произведение равно
. Их скалярное произведение равно 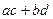 . теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол
. теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол 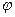 .
.
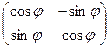
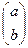 =
= 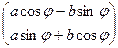
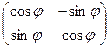
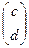 =
= 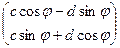
А теперь скалярно перемножим 2 получившихся вектора:
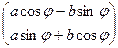 и
и 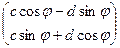 .
.
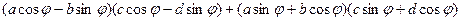 =
=
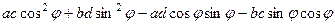 +
+
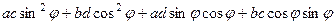
Учитывая, что 3,4,7,8 слагаемые взаимоуничтожаются, получим:
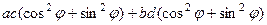 =
= 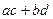 .
.
Что и требовалось доказать.
Итак, 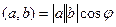 .
.
Свойства нормы (модуля):
1) 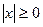
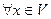 , причём
, причём 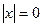
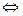
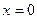 ,
,
2) 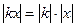
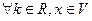 ,
,
3) 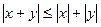 (неравенство Минковского).
(неравенство Минковского).
Для его доказательства покажем, что 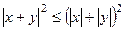 .
.
Рассмотрим 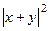 =
= 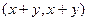 =
= 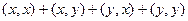 =
=
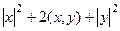 =
= 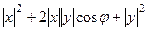
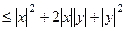 =
= 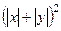 . Итак,
. Итак, 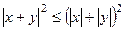
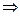
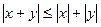 .
.
Дата добавления: 2021-01-11; просмотров: 682;











